Page 76 - 《应该声学》2022年第2期
P. 76
244 2022 年 3 月
障分类。
0 引言
1 检测信号的提取及分割
扬声器异常声检测是扬声器出厂前必须进行
的重要流程。传统的异常声检测采用专业声音检 扬声器异常声可能由多种问题产生;在本研究
听员以人耳检测为主,由于检听员存在易疲劳、主 中针对普通扬声器的异常声样本与合格样本进行
观性强、长时间工作损害听觉系统等问题,传统检 区分。根据扬声器特性以及检测需求,设计对数回
测方法已很难满足高精度、大批量快速检测的需 扫信号激励扬声器发声;经传声器声电转换后由采
求 [1] 。近年来大量学者对扬声器异常声检测方法进 集卡采集,截取信号有效数据做短时傅里叶变换得
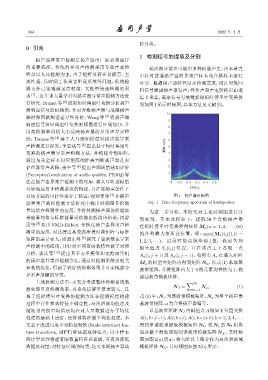
行研究,Brunet等 [2] 应用短时傅里叶变换分析扬声 到如图1所示时频图,具体方法见文献[5]。
器响应信号的时频图,并对合格扬声器与故障扬声
10
器时频图做频谱差异性分析;Wang 等 [3] 将扬声器
9
响应信号短时傅里叶变换时频图进行区域划分,并
8
用高阶频率均值大小反映扬声器的异常声差异程
7
度;Temme 等 [4] 基于人耳感知模型对扬声器异常 6
声检测进行探究;李宏斌等 [5] 提出基于短时傅里叶 ᮠဋ/kHz 5
变换的扬声器异常声检测方法,并构建分割矩阵, 4
通过与黄金样本对应矩阵的距离判断扬声器是否 3
存在异常声故障;张平等 [6] 提出声频质量感知评价 2
(Perceptual evaluation of audio quality, PEAQ)算 1
法在扬声器异常声检测中的应用,将人耳听觉模型 0 0.1 0.2 0.3 0.4 0.5
巧妙地应用于检测系统的构建,并在实验室条件下 ᫎ/s
对该方法的可行性进行了验证;祝仰宽等 [7] 在扬声 图 1 扬声器时频图
器异常声故障检测方法研究中提出时频图各阶能 Fig. 1 Time-frequency spectrum of loudspeaker
量均值在检测中的应用,并将待测扬声器各阶谐波 为进一步分析,本研究对上述时频图进行分
带能量均值与标准能量差值做比较得出结论;周静 割处理。基本过程如下:提取 50 个合格扬声器
雷等 [8] 提出 VMD-Hilbert 变换在扬声器异常声检
经短时傅里叶变换所得矩阵 M a (a = 1, 2, · · · , 50)
测中的应用,对比得出其变换所得时频矩阵与标准
的各列最大值所在位置,即:max(M a (i,j)),(i =
矩阵的差异更大;周晓东等 [9] 探究了窗函数在异常 1, 2, 3, · · · ), 记录对应点纵坐标 j 值, 确定各列
声检测中的应用,并针对不同窗函数特性做了对照 极大值点 A a (i,j) 位置,并在该点上下各取一点
分析;郭庆等 [10] 提出基于心里模型和支持向量机 A a (i, j + 1) 及 A a (i, j − 1),将所有 A a 点填入矩阵
的扬声器异常声检测方法,通过对检测系统及相关 M a 的同型零矩阵内得到矩阵 N a ,以式 (1) 求取基
参数的优化,得到了较好的检测效果并可实现部分 波带矩阵,并将矩阵内大于 0 的元素均替换为 1,构
异常声故障的分类。
建基波带模板矩阵。
上述检测方法中,未充分考虑整体检测系统数 ∑ 50
N J = N a , (1)
据处理量及检测效率,对系统运算量要求较大。且 a=1
基于短时傅里叶变换的检测方法在检测模型构建 式(1)中,N J 为基波带模板矩阵,N a 为单个扬声器
过程中存在有效特征不确定性,高次谐波均值法及 基波带矩阵,a为合格扬声器编号。
谐波带内能量均值法均在对大量数据进行平均化 以基波带矩阵 N J 内赋值点 A做如下位置变换
处理的基础上进行,使有效特征被平均化处理。本 A(i, b×j−1),A(i, b×j),A(i, b×j+1),b = 2, 3, 4, · · ·
文基于改进尺度不变特征转换(Scale-invariant fea- 得到单谐波带提取模板矩阵 N b ,将 N 1 至 N 7 相叠
ture transform, SIFT) 算法提取特征点,以小样本 加并做平滑处理得到谐波带模板矩阵 N X ,其时频
统计学原理构建有限数量特征点模板,可有效降低 图如图 2(a) 所示;将七阶以上部分作为高次谐波域
数据处理量;对特征区域的归类,还可实现扬声器故 模板矩阵N G ,其时频图如图2(b)所示。