Page 101 - 《应用声学》2022年第4期

第 41 卷 第 4 期 石志奇等： Hudson 模型适用性及储层微观建模应用 599

其中， 式(12)中，α m (m = 1, 2, 3)为Biot-Willis系数，α 4 =
µ m 9K m + 8µ m α 5 = α 6 = 0；K m 、K f 分别为固体基质和流体的体
ζ m = , (10)
积模量；φ为孔隙度。
6 K m + 2µ m
式 (10) 中，K m 、µ m 分别为背景基质的体积模量和
剪切模量；x i 为第i种包含物的体积含量；P mi 、Q mi
3 实际资料应用
为第 i 种包含物的形状参数，不同形状包含物的参
数可参见Berryman [21] 。 选取某地区一口井的实际测井资料，利用图 5
2.3 BK 模型 所示的裂缝型储层建模流程以及第2 节所介绍的模

利用适用于各向异性条件下的 BK 模型添加 型构建裂缝储层等效岩石物理模型，以分析利用
混合流体计算饱和岩石的弹性模量。该模型是由 Hudson 模型在微观储层建模中的适用条件。岩石
Brown 等 [22] 对各向同性的 Gassmann 公式的推广。 矿物的弹性参数参照岩石物理手册 [24] 中相关数据，
将饱和各向异性岩石的刚度矩阵表示为干燥各向 如表2所示。
异性岩石的刚度矩阵与因饱含流体而产生附加修
正项之和，表达式为 表 2 矿物及流体的弹性模量 [24]
dry
sat
∗
C ij = C ij + α i α j M , (11) Table 2 Elastic modules of minerals and
fluids [24]
式 (11) 中，C sat 、C dry (i, j = 1, 2, · · · , 6) 分别为各
ij ij
向异性岩石在饱和、干燥状态下的刚度矩阵；α 为 矿物 石英 泥质 长石
体积模量/GPa 37.0 21.0 37.5
Biot-Willis系数 [23] 。α、M 、K 表达式为
∗
∗
 剪切模量/GPa 44.0 9.0 15.0
3
 1 ∑
 dry
 C ,
α m = 1 − nm

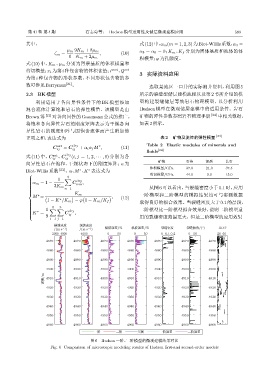
 3K m 从图 6 可以看出，当裂缝密度小于 0.1 时，应用
 n=1



 K m 一阶模型和二阶模型的模拟结果均可与实测数据
∗ ),
M = ( ) ( (12)
∗
1 − K /K m − φ 1 − K m /K f
 取得良好的拟合效果。当裂缝密度大于 0.1 的层段，


 3 3

 1 ∑ ∑ 二阶模型比一阶模型拟合效果好，说明二阶模型适
 dry
∗
K = C ,

 ij
 9 用的裂缝密度范围更大，但是二阶模型的应用效果
i=1 j=1
ഷฉᤴए ጫฉᤴए
/(mSs -1 ) /(mSs -1 ) ഷฉឨࣀ/% ጫฉឨࣀ/% ᜈᎋࠛए ᜈᎋϚᝈ/(°) HDT
2000 4000 4000 0 50 0 50 0 0.1 0.2 0 50 20 60
4870 4870 4870 4870 4870 4870 4870
4880 4880 4880 4880 4880 4880 4880
4890 4890 4890 4890 4890 4890 4890
4900 4900 4900 4900 4900 4900 4900
ງए/m 4910 4910 4910 4910 4910 4910 4910
4920 4920 4920 4920 4920 4920 4920
4930 4930 4930 4930 4930 4930 4930
4940 4940 4940 4940 4940 4940 4940
4950 4950 4950 4950 4950 4950 4950
4960 4960 4960 4960 4960 4960 4960
ʷ᫽ ̄᫽ ࠄ฾ ʷ᫽ឨࣀ ̄᫽ឨࣀ
图 6 Hudson 一阶、二阶模型的微观建模结果对比
Fig. 6 Comparison of microscopic modeling results of Hudson first-and second-order models