Page 72 - 《应用声学》2022年第4期

570 2022 年 7 月

6310 m 深度波形 (见图 1(a) 中区域 C) 相干分析的 外反射体特征。而一般而言，经过叠加后，反射信
结果，得到其下行视速度为 3100 m/s 左右，验证其 号得到一定程度的增强，这些噪声特征会减弱，总
为沿井轴传播的反射横波。 体表现为非相干性，但其仍然会掩盖部分真实反射
以上分析表明，随机噪声、残余模式波和井孔 波。因此采取适当的滤波方法进一步压制噪声并增
模式波反射存在于远探测声波测井的波形中，尤其 强反射信号是实际中需要解决的关键难题。针对该
是沿井轴传播的反射干扰常被误以为是井外反射。 问题，本文引入各向异性扩散滤波方法来进行处理
这些噪声的存在，使获取的图像难以表示真正的井 分析。

4000
3500
ᤴए/(mSs -1 ) 2500
3000
6180 2000
1500
6200 1000
500
6220 2.2 2.4 2.6 2.8 3.0 3.2 3.4 3.6 3.8
௑ᫎ/ms
(b) ӝ۫AᄱࣰѬౢፇ౧
6240
4000
B
3500
6260 3000
ງए/m 6280 ᤴए/(mSs -1 ) 2500
2000

6300 1500
1000
C 500
2.16 2.18 2.20 2.22 2.24 2.26
6320
௑ᫎ/ms
(c) ӝ۫BᄱࣰѬౢፇ౧
6340
4000
A
3500
6360 3000
ᤴए/(mSs -1 ) 2500
0 10 20 30 2000
௑ᫎ/ms 1500
(a) Ԧ࠱ฉѬሏՑҖ᭧ 1000
500
1.86 1.88 1.90 1.92 1.94 1.96 1.98 2.00
௑ᫎ/ms
(d) ӝ۫CᄱࣰѬౢፇ౧

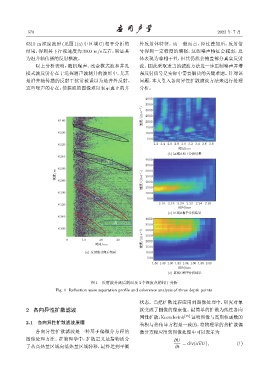
图 1 反射波分离后剖面及 3 个深度点的相干分析
Fig. 1 Reflection wave separation profile and coherence analysis of three depth points

状态。当把扩散过程应用到图像处理中，研究对象
2 各向异性扩散滤波 就变成了图像的像素值。最简单的扩散为线性各向
同性扩散，Koenderink [15] 证明图像与高斯核函数的
2.1 各向异性扩散滤波原理
卷积与热传导方程是一致的，将物理学的热扩散偏
各向异性扩散滤波是一种基于偏微分方程的 微分方程应用到图像处理中可以表示为
图像处理方法。在物理学中，扩散定义是指物质分 ∂U
= div(a∇U), (1)
子从高热量区域向低热量区域转移，最终达到平衡 ∂t