Page 80 - 《应用声学》2022年第6期

926 2022 年 11 月

3.2.1 次级声源选点位置比较 40
LS-Uniவขေ᝷ϙ
不同频率工况下，CVXL1 方法和 CMP 算法的 35 LS-Uniவขࠄᰎϙ
CVXL1வขေ᝷ϙ
次级声源选点结果如图 5 所示，图中蓝色三角表示 30 CVXL1வขࠄᰎϙ
CMPவขေ᝷ϙ
CVXL1 方法选中的次级声源位置，红色圆点表示 25 CMPவขࠄᰎϙ
CMP算法选中的次级声源位置。作为对比，图5(a)、 ᬌ٪᧚/dB 20
图 5(d)、图 5(g)、图 5(j) 列出了不同频率下次级声 15
源均匀布放的最小二乘 (Least-squares algorithm 10
with the uniformly placed secondary sources, LS- 5
Uni) 算法的次级声源位置 (紫色圆点)。从图 5(a)∼ 0
200 400 600 800 1000 1200 1400 1600 1800
图5(l) 的对比可看出，与均匀布放的次级声源相比， ᮠဋ/Hz
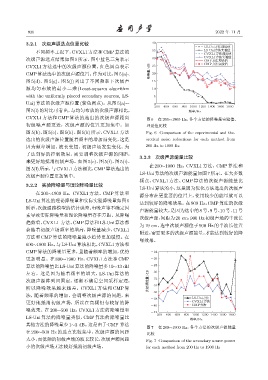
CVXL1 方法和 CMP 算法的选出的次级声源距离 图 6 在 200∼1900 Hz，各个方法的降噪量实验值、
初级噪声源更近，次级声源的位置更加集中。如 理论值比较
图 5(b)、图 5(e)、图 5(h)、图 5(k) 所示，CVXL1 方法 Fig. 6 Comparison of the experimental and the-
选出的次级声源位置随着频率的增加而变化，这是 oretical noise reductions for each method from
因为频率增加，波长变短，初级声场发生变化，为 200 Hz to 1900 Hz
了达到好的控制效果，需要调整次级声源的间距，
3.2.3 次级声源能量比较
来更好地抵消初级声场。如图 5(c)、图 5(f)、图 5(i)、
在 200∼1900 Hz，CVXL1 方法、CMP 算法和
图 5(l)所示，与CVXL1方法相比，CMP算法选出的
LS-Uni算法的次级声源能量如图 7 所示。在大多数
次级声源位置更加集中。
频点，CVXL1 方法、CMP 算法的次级声源能量比
3.2.2 实验降噪量与理论降噪量比较
LS-Uni 算法的小，这是因为优化方法选出的次级声
在 200∼1900 Hz，CVXL1 方法、CMP 算法和
源分布在更重要的位置上，使用较少的能量就可以
LS-Uni算法的理论降噪量和实际实验降噪量如图6
达到较好的降噪效果。在900 Hz，CMP算法的次级
所示，次级通路模型的估计误差、电噪声等不确定因
声源能量较大，是因为选中的8 号、9 号、10号、11号
素导致实际降噪量和理论降噪量存在差距。从降噪
次级声源，间距为 20 cm，900 Hz初级声场的半波长
趋势看，CVXL1 方法、CMP 算法和 LS-Uni 算法都
为 19 cm，选中次级声源位于 900 Hz 的半波长位置
会随着初级声场频率的增高，降噪量减少，CVXL1
附近，需要更多的次级声源能量，才能达到较好的降
方法和 CMP 算法的降噪量减小趋势更加缓慢。在
噪效果。
600∼1900 Hz，与 LS-Uni 算法相比，CVXL1 方法和
CMP 算法的降噪量更多，且随着频率的增加，优势 -24
更加明显。在 800∼1900 Hz，CVXL1 方法和 CMP -26
算法的降噪量比LS-Uni算法的降噪量多10∼13 dB -28
左右。这是因为随着频率的增大，LS-Uni 算法的 -30
次级声源阵列间固定，逐渐不满足空间采样定理， ൓ጟູᑟ᧚/dB -32
所以降噪效果越来越差。CVXL1 方法和 CMP 算 -34
法，随着频率的增加，会调整次级声源的间距，来 -36
-38 LS-Uniவข
更好地抵消初级声场，所以在高频仍有较好的降 CVXL1வข
-40 CMPவข
噪效果。在 200∼500 Hz，CVXL1 方法的降噪量和
-42
200 400 600 800 1000 1200 1400 1600 1800
LS-Uni 算法的降噪量类似，CMP 算法的降噪量比
ᮠဋ/Hz
其他方法的降噪量少1∼2 dB。这是由于CMP 算法
图 7 在 200∼1900 Hz，各个方法的次级声源能量
在 200∼500 Hz 的选点比较集中，次级声源的间距 比较
太小，而低频的初级声场的波长较长，次级声源间距 Fig. 7 Comparison of the secondary source power
小的次级声场无法较好抵消初级声场。 for each method from 200 Hz to 1900 Hz