Page 194 - 《应用声学》2023年第2期

382 2023 年 3 月

લՌజ᭧ˁࠄᰎ஝૶
T10 4 ࠄᰎ஝૶Ѭࣱ࣋᭧
800
2.055
600
z
400
2.050
200
2.045
2.04 2.02 500 1000
y⊳ᮠဋ஝૶ག 2.040 ஝૶ቇᫎѬ࣋ 0 x
yT10 4

2.035

2.030 400
z⊳ႃ᫾஝૶ག 200
2.025 0

2.020 -200
0 200 400 600 800 1000 2.04 1000
500
x⊳ႃԍ஝૶ག yT10 4 2.02 0 x
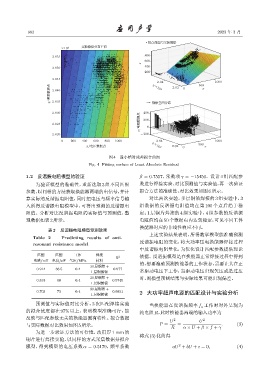
图 4 最小绝对残差拟合曲面
Fig. 4 Fitting surface of Least Absolute Residual

1.2 反谐振电阻模型的验证 β = 0.7557，常数项 γ = −15450。设计 4 组匹配参
为验证模型的准确性，重新选取 3 组不同匹配 数进行焊接实验，对比预测值与实验值，再一次验证
参数，以同样的方法获取换能器两端的电信号，并计 拟合方法的准确性，对比效果如图6所示。
算实际的反谐振电阻值，同时把电压与频率信号输 对比两次实验，多层铜箔焊接的 3 组实验中，3
入所得反谐振电阻模型中，可得出预测的反谐振电 组数据的反谐振电阻值均在第 100 个点后趋于稳
阻值。分析对比反谐振电阻的实际值与预测值，整 定；1 层铜片焊接的 4 组实验中，4 组参数的反谐振
理数据如表2所示。 电阻值均在50个数据点内达到稳定，可见不同工件
换能器对应的非线性响应不同。
表 2 反谐振电阻模型预测效果
上述实验结果表明，所得数学模型能准确预测
Table 2 Predicting results of anti-
反谐振电阻的变化，将大功率压电换能器焊接过程
resonant resistance model
中反谐振电阻量化，为优化设计匹配参数提供理论
匹配 匹配 工作 焊接 依据。反谐振模型是在换能器正常焊接过程中得到
R 2
电感/mH 电容/nF 气压/MPa 材料
的，想要准确预测换能器的工作状态，需要让其在正
30 层铜箔 +
0.914 38.5 0.4 0.977
1 层铜镀镍 常驱动电压下工作，当驱动电压出现欠压或是过压
30 层铜箔 + 时，则模型预测结果与实际结果可能出现偏差。
0.818 60 0.4 0.9745
1 层铜镀镍
30 层铜箔 +
0.703 73 0.4 0.9851 2 大功率超声电源的匹配设计与实验分析
1 层铜镀镍
预测值与实际值对比分析，3 次匹配焊接实验 当换能器在反谐振频率 f a 工作时对外呈现为
的拟合优度都在 97% 以上，表明模型准确可行，能 纯电阻R，此时换能器两端的输入功率为
反映与匹配参数无关的换能器固有特性。拟合数据 2 2
U U
与实际数据对比效果如图5所示。 P = = . (3)
R α × U + β × f + γ
为进一步验证方法的可行性，改用厚 1 mm 的
将式(3)化简得
铜片进行焊接实验，以同样的方式采集数据并拟合
2
模型，得到模型的电压系数 α = 0.5179，频率系数 aU + bU + c = 0, (4)