Page 32 - 《应用声学》2023年第2期

220 2023 年 3 月

主要原因是任何的骨架模量只会增加多孔介质的 频率 (1 kHz 左右) 处等效密度的虚部较大。当频率
体积模量。图 2 给出了利用 Biot-Stoll 理论预测的 很低时，多孔介质中孔隙流体和骨架没有相对运
快纵波衰减系数和 EDFM 模型预测的衰减系数与 动，等效密度的实部接近沉积物真实密度；当频率
频率关系对比，除了在较低的频率处有较小的差别 很高时，骨架的运动幅度小于孔隙流体的运动幅度，
外，其他频率范围内两者基本一致。由于与骨架模 产生相对运动，等效密度的实部小于沉积物真实
量相关的衰减系数与频率是线性关系，而由于水的 密度。
黏滞特性引起的衰减系数在低频段与频率是平方
2.2 Biot-Stoll和EDFM计算的反射系数对比
关系，因此当频率很低时，衰减系数的主要贡献是骨
根据表 1 给出的海底底质参数，分别利用 Biot-
架模量。
Stoll模型和EDFM方法计算海水-海底界面的反射
图 3 给出了砂质海底的真实密度与等效密度
系数。当海底为多孔弹性介质时，采用 Biot-Stoll 模
的实部和虚部对比。从图 3 中可知在低频时等效
型计算海水-海底界面的反射系数，计算方法采用波
密度的实部与真实密度基本一致，而在较高频率
数积方法 [18] ；当海底为EDFM 时，海底看作液态海
时等效密度的实部小于真实密度；在频率较低和
底，海底的等效密度和声速分别通过公式 (13) 和公
频率较高时，等效密度的虚部较小，在 Biot 的特征
式 (16) 得到，反射系数计算采用 Rayleigh 反射公式
计算：
10 2
ρ 2 c 2 / sin θ 2 − ρ 1 c 1 / sin θ 1
R = , (17)
ρ 2 c 2 / sin θ 2 + ρ 1 c 1 / sin θ 1
0
10
ᛰѓጇ஝/(dBSm -1 ) 10 -2 底 的 密 度， c 1 和 c 2 分 别 为 海 水 和 海 底 的 声 速，
其中，R 为反射系数，ρ 1 和 ρ 2 分别为海水和海
θ 1 和 θ 2 分 别 为 入 射 角 和 折 射 角， 其 关 系 式 为

Biot-Stollေ᝷
-4
10
图 4 给 出 了 Biot-Stoll 计 算 的 反 射 系 数 和
኎஍ࠛएืʹവی(EDFM) cos θ 1 /c 1 = cos θ 2 /c 2 。
EDFM 模型计算的反射损失和相位的比较，在频
10 -6
10 1 10 2 10 3 10 4 10 5 10 6 率分别为 10 Hz、200 Hz、2 kHz 和 20 kHz 时可知
ᮠဋ/Hz
两种方法计算的反射系数基本一致，这也表明了
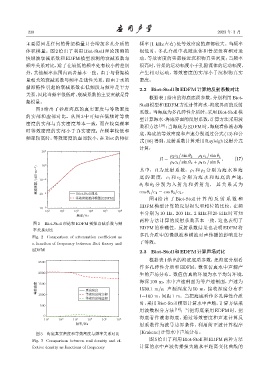
图 2 Biot-Stoll 理论和 EDFM 预报衰减系数与频
EDFM 的准确性。反射系数结果也表明 EDFM 将
率关系对比
多孔介质中的慢纵波和横波对声传播的影响进行
Fig. 2 Comparison of attenuation coefficient as
a function of frequency between Biot theory and 了等效。
EDFM
2.3 Biot-Stoll和EDFM计算声场对比
根据表 1 给出的海底底质参数，把海底分别看
2500
作多孔弹性介质和 EDFM，数值仿真水中声源产
2000 生的声场分布。数值仿真的环境为水平均匀环境，
海深 100 m，水中声速剖面为等声速剖面，声速为
኎஍ࠛए ᄾࠄࠛए 1530.1 m/s；声源深度为 50 m，接收深度分布在
1500
1000 ኎஍ࠛएᄊࠄᦊ 1∼100 m，间距 1 m。当把海底看作多孔弹性介质
኎஍ࠛएᄊᘿᦊ
时，采用 Biot-Stoll 模型计算水中声场，计算方法采
500
用波数积分方法 [18] ；当把海底采用 EDFM 时，把
0 海底看作液态海底，通过等效密度和声速计算反
10 1 10 2 10 3 10 4 10 5 10 6
ᮠဋ/Hz 射系数作为波导边界条件，利用简正波计算程序

图 3 海底真实密度和等效密度与频率关系对比 (Krakenc)计算水中声场分布。
Fig. 3 Comparison between real density and ef- 图 5 给出了利用 Biot-Stoll 和 EDFM 两种方法
fective density as functions of frequency 计算的水中声波传播损失随水平距离变化曲线的