Page 35 - 《应用声学》2023年第2期

第 42 卷 第 2 期 李鹏等： 基于等效密度流体模型的地声参数分析 223

2.4 EDFM与地声反演参数等价分析 密度实部和真实密度基本一致，而等效密度的虚部
通过前面 EDFM分析可知，在多孔介质弹性海 为零。图9给出了基于砂质海底计算的反射系数，其
底模型，海底的快纵波声速可用EDFM 纵波声速代 中绿色点线是将 EDFM 中的等效密度用真实密度
替，快纵波的衰减系数可用等效流体模型的纵波衰 代替。从图 9 中可以看出对于较低频率时，采用真
减系数代替。但是由于 EDFM 的等效密度是复数， 值密度计算的反射系数损失和相位与 EDFM 计算
那么是否可以用真实密度代替？如果能够利用真实 反射系数基本一致，频率较高和小掠射角时，计算
密度代替，那么 EDFM 就等价于液态海底模型，即 的反射系数也基本一致；但是频率较高和大掠射角
可与通常采用的 Hamilton 地声模型相互等价。从 时，采用真实密度计算的反射损失小于EDFM计算
图3 中可知，当频率在 1 kHz 以下时，EDFM中等效 的反射损失。

10
10
Ԧ࠱૯ܿ/dB 5 Biot-Stollေ᝷ Ԧ࠱૯ܿ/dB 5 Biot-Stollေ᝷
኎஍ࠛएืʹവی(EDFM)
኎஍ࠛएืʹവی(EDFM)
0 ืʹവی(኎஍ܦᤴ֗ᛰѓnjᄾࠄࠛए) 0 ืʹവی(኎஍ܦᤴ֗ᛰѓnjᄾࠄࠛए)
0 10 20 30 40 50 60 70 80 90 0 10 20 30 40 50 60 70 80 90
ଉ࠱ᝈ/(O) ଉ࠱ᝈ/(O)
200 200
ᄱͯ/(O) 150 ᄱͯ/(O) 100
100
50 0
0 -100
0 10 20 30 40 50 60 70 80 90 0 10 20 30 40 50 60 70 80 90
ଉ࠱ᝈ/(O) ଉ࠱ᝈ/(O)
(a) 10 Hz (b) 200 Hz
10 10
Ԧ࠱૯ܿ/dB 5 Biot-Stollေ᝷ Ԧ࠱૯ܿ/dB 5 Biot-Stollေ᝷

኎஍ࠛएืʹവی(EDFM)
኎஍ࠛएืʹവی(EDFM)
0 ืʹവی(኎஍ܦᤴ֗ᛰѓnjᄾࠄࠛए) 0 ืʹവی(኎஍ܦᤴ֗ᛰѓnjᄾࠄࠛए)
0 10 20 30 40 50 60 70 80 90 0 10 20 30 40 50 60 70 80 90
ଉ࠱ᝈ/(O) ଉ࠱ᝈ/(O)
200 200
ᄱͯ/(O) 100 0 ᄱͯ/(O) 100 0

-100 -100
0 10 20 30 40 50 60 70 80 90 0 10 20 30 40 50 60 70 80 90
ଉ࠱ᝈ/(O) ଉ࠱ᝈ/(O)
(c) 2 kHz (d) 20 kHz
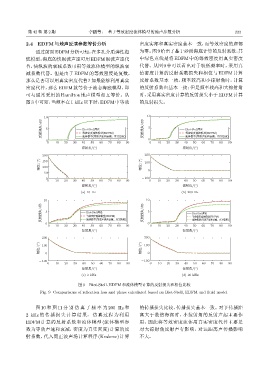
图 9 Biot-Stoll、EDFM 和流体模型计算的反射损失和相位比较
Fig. 9 Comparisons of reflection loss and phase calculated based on Biot-Stoll, EDFM and fluid model

图 10 和 图 11 分 别 仿 真 了 频 率 为 200 Hz 和 的传播损失比较，传播损失基本一致。对于传播距
2 kHz 的传播损失计算结果， 仿真过程为利用 离大于数倍海深时，小掠射角的反射声起主要作
EDFM 计算的反射系数和流体模型 (流体模型参 用，因此将等效密度流体用真实密度代替主要是
数为等效声速和衰减，密度为真实密度) 计算的反 对大掠射角反射声有影响，对远距离声传播影响
射系数，代入简正波声场计算程序 (Krakenc) 计算 不大。