Page 40 - 《应用声学》2023年第2期

228 2023 年 3 月

( ) 2
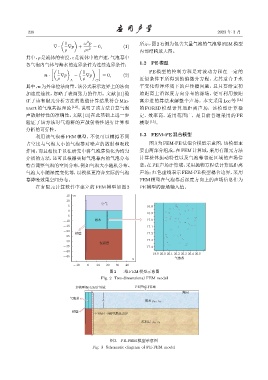
1 ω p 所示，图2 右侧为包含大量气泡的气泡幕FEM模型
∇ · ∇p + 2 = 0, (1)
ρ ρc 内部结构放大图。
其中，ρ是流体的密度，c是流体中的声速，气泡幕中
各气泡内气体与海水的边界条件为连续边界条件： 1.2 PE模型
[( ) ( ) ]
1 1 PE 模型的控制方程是对波动方程在一定的
n · ∇p − ∇p = 0, (2)
ρ ρ 近似条件下所得到的偏微分方程，尤其适合于水
L G
其中，n为外单位法向量。该公式表示边界上的法向 平变化海洋环境下的声传播问题，且只要给定初
加速度连续，忽略了表面张力的作用。文献 [11] 验 始距离上沿深度方向分布的源场，便可利用按距
证了该有限元分析方法的数值计算结果符合 Min- 离步进的算法求解整个声场。本文采用 Lee 等 [14]
naert 的气泡共振理论 [12] ，说明了该方法计算气泡 的 FOR3D 模型计算远距离声场，该模型计算稳
声散射特性的准确性，文献 [13] 在此基础上进一步 定、效率高、适用范围广，是目前普遍采用的 PE
验证了该方法对气泡群的声散射特性进行计算和 模型 [15] 。
分析的可行性。
利用该气泡幕 FEM 模型，不仅可以模拟不同 1.3 FEM-PE混合模型
占空比与气泡大小的气泡幕对噪声的散射和吸收 图 3 为 FEM-PE 法混合模型示意图，该模型主
作用，而且相较于以往研究中将气泡幕简化为均匀 要由两部分组成，在 FEM 计算域，采用有限元方法
介质的方法，还可以根据实际气泡幕内的气泡分布 计算桩体振动特性以及气泡幕邻近区域的声场信
特点调整气泡的空间分布，例如气泡大小随机分布、 息；在 PE 声场计算域，采用抛物方程法计算远距离
气泡大小随深度变化等，以模拟更符合实际的气泡 声场；红色虚线表示 FEM-PE 模型耦合边界，采用
幕降噪效果空间分布。 FEM 模型在气泡幕后深度方向上的声场信息作为
在有限元计算软件中建立的 FEM 模型如图 2 PE模型的源场输入值。

15 m
10
ቇඡ
5 16.8
0
16.9
-5
-10 ๒ඵ 17.0
-15 17.1
-20
ೈܞ 17.2
-25
-30 17.3
ොሥࡏ
-35 17.4
-40
19.9 20.0 20.1 20.2 20.3 20.4 20.5
-45
m ඡจ࣫
-10 0 10 20 30 40
图 2 二维 FEM 模型示意图
Fig. 2 Two-dimensional FEM model

ܳྭေڤFEMᝠካ۫ PEܦڤᝠካ۫
๒᭧
ඡจ࣫
h ๒ඵ ρ w֒ c w

ೈܞ
FEM-PEവیᏹՌ᣸ႍ
ොሥࡏ ρ b֒ c b

图 3 PE-FEM 模型示意图
Fig. 3 Schematic diagram of PE-FEM model