Page 46 - 《应用声学》2023年第2期

234 2023 年 3 月

大于共振频率时，不同占空比的气泡幕的等效衰减 式 (4) 中， λ 用 以 指 代 为 气 泡 群 的 中 心 半 径 a，
系数存在明显差别。利用参考文献 [8] 中的气泡幕 λ = 10a；k 用以指代为气泡群中各气泡的半径 b，
等效声衰减系数计算方法，在图 11(b) 中给出了不 k = 10b, b = 0, 0.1, 0.2, · · · ，这样式 (4) 可表示为中
同占空比气泡幕 10 Hz∼100 kHz 频段等效声衰减 心半径为a的泊松分布气泡半径概率函数。图13为
系数曲线，可见在大于共振频率的中高频段，高占空 建立的气泡大小泊松分布的气泡幕的建模结果及
比气泡幕的声衰减系数显著更大。 各半径气泡数量分布图，中心半径为 4.5 mm，占空
当气泡幕的占空比很小 (在 0.5% 附近) 时，在 比5%。
大于截至频率的频段的降噪效果会急剧降低，高
10 4
占空比的气泡幕具有明显优势。由图 11(a) 可以看
2.0 mm
出，占空比0.5%的气泡幕的降噪量在噪声频率大于 4.5 mm
10 3 7.3 mm
750 Hz 时迅速下降，因此气泡幕的占空比不宜设置
过小，至少应大于 1%，否则会使较高频段的降噪效 ce/(mSs -1 Ď 10 2
果大打折扣。另外，占空比分别为 1% 和 2.5% 的两
种气泡幕的降噪效果始终没有很大差别，在较大占 10 1
空比的情况下，继续提高占空比对气泡幕的降噪效
果的提升有限。 10 0 10 1 10 2 10 3 10 4 10 5
ᮠဋ/Hz
2.3.4 气泡幕内气泡半径
(a) ˀՏඡจӧय़ඡจ࣫ᄊ኎஍ܦᤴజጳ
利用参考文献 [8] 中的气泡幕等效声速计算
40
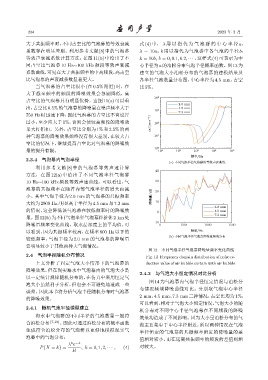
方法，在图 12(a) 中给出了不同气泡半径气泡幕
10 Hz∼100 kHz 频段等效声速曲线。可以看出，气 30
泡幕的共振频率在随着内部气泡半径的增大而减 20
小。其中气泡半径为 2.0 mm 的气泡幕的共振频率 ᬌ٪᧚/dB
大约为2900 Hz，明显高于半径为4.5 mm与7.3 mm 10
2.0 mm
的情况，这会降低该气泡幕在较低频率时的降噪效 0 4.5 mm
7.3 mm
果。图12(b)为不同气泡半径气泡幕距桩体 2 km处
-10
降噪量频率变化曲线。取水层深度上的平均值，可 0 500 1000 1500
以看到，因为共振频率较高，在频率 800 Hz 以下的 ᮠဋ/Hz
(b) ˀՏඡจӧय़ඡจ࣫ᬌ٪᧚ᮠ۫Ѭ࣋
较低频率，气泡半径为 2.0 mm 的气泡幕的降噪量
要明显较小于其他两种大气泡情况。
图 12 不同气泡半径气泡幕降噪量频率变化曲线
2.4 气泡半径随机分布情况 Fig. 12 Frequency domain distribution of noise re-
上文分析了固定气泡大小情形下的气泡幕的 duction value of air bubble curtain with air bubble
降噪效果，但在现实海水中气泡幕内的气泡大小是
2.4.2 与气泡大小恒定情况对比分析
以一定统计规律随机分布的，在仿真中采用恒定气
图 14 为气泡幕内气泡半径恒定情况与泊松分
泡大小虽然利于分析，但也会不可避免地造成一些
布情况频域降噪曲线对比。分别取气泡中心半径
误差。因此本节将分析气泡半径随机分布时气泡幕
2 mm、4.5 mm、7.3 mm 三种情况，占空比均为 1%，
的降噪效果。
可以看到，相对于气泡大小恒定情况，气泡大小的随
2.4.1 随机气泡半径模型建立
机分布对不同中心半径气泡幕在不同频段的降噪
海水中气泡群的不同半径的气泡数量一般符 效果均造成了不同影响。因为大小呈泊松分布的气
合泊松分布 [7,19] 。因此可通过泊松分布的概率函数 泡主要集中于中心半径附近，所以两种情况在气泡
生成符合泊松分布的气泡群以更好地模拟现实气 半径恒定的气泡幕的共振频率附近的降噪量的差
泡幕中的气泡分布：
值相对较小，而在远离共振频率的频段的差值则相
k −λ
λ e
P{X = k} = , k = 0, 1, 2, · · · , (4) 对较大。
k!