Page 176 - 《应用声学》2023年第3期

614 2023 年 5 月

本不会造成共振频率的偏移。同时，由于耦合效应 下组合结构的STL谱线，如图2(c)所示。其中，蓝色
的存在，组合结构共振频率附近的 STL 有了较为明 实线为将 3 个单元按照 1 号、2 号和 3 号的顺序依次
显的提升，其最终的隔声效果并不是每个单元隔声 排列后的组合结构 (以下简称 “1-2-3” 组合) 的 STL
量的简单叠加。 谱线；黄色虚线为将 3 个单元按照 1 号、3 号和 2 号
的顺序依次排列后的组合结构(以下简称“1-3-2”组
表 2 3 个 THR 单元的几何参数及共振频率
合) 的 STL 谱线；绿色点线为将 3 个单元按照 2 号、
Table 2 Geometric parameters and reso-
1 号和 3 号的顺序依次排列后的组合结构 (以下简
nance frequencies of the three THRs
称 “2-1-3” 组合) 的 STL 谱线。对比 “1-3-2” 组合的
STL 谱线和另外两条谱线，可以看到 “1-3-2” 组合
结构 1 结构 2 结构 3
的 STL 谱线在 251 Hz 处的共振峰的高度明显低于
a 1 /cm 1.38 1.89 1.98
另外两条谱线。该共振峰为1 号单元的一阶共振峰，
l 1 /cm 1.12 0.53 0.13
且与 2 号单元的一阶共振峰在频率上较为接近。而
h 1 /cm 6.85 10.82 8.58
在 “1-3-2” 组合中，1 号单元和 2 号单元间放置了一
a 2 /cm 0.96 1.12 0.83
个 3 号单元，导致两个单元相距较远，因此这两个
l 2 /cm 3.88 2.35 3.59
共振峰间的耦合效应被削弱了，致使“1-3-2”组合在
h 2 /cm 1.88 3.89 1.87
251 Hz处的共振峰的高度更接近于1号单元原本的
f 1 /Hz 251 245 275
一阶共振峰的高度，并没有因为耦合效应的存在有
f 2 /Hz 430 454 504
所提升。类似的效应也存在于 “2-1-3” 组合第五个
其次，改变了组合结构单元之间的间距 L，基 共振峰和第六个共振峰的中间区域，在这个频带内
于 FEM 计算了不同单元间距的组合结构的 STL “2-1-3” 组合的 STL 谱线较另外两条谱线相比出现
频谱， 如图 2(b) 所示。其中， 蓝色实线为间距 了很明显低谷。这其实是因为组合中 2 号单元和 3
L = 15 cm 时组合结构的 STL 频谱，黄色虚线为 号单元距离较远，因此 2 号单元的二阶共振峰和 3
间距 L = 20 cm 时组合结构的 STL 频谱，绿色点线 号单元的二阶共振峰间的耦合效应被虚弱了，导致
为间距 L = 25 cm 时组合结构的 STL 频谱。观察 组合结构在该频率区间的STL较低。
图 2(b) 的 3 条曲线可知，改变单元之间的间距依然 综上所述，由于耦合效应的存在，对组合结构
不会造成共振频率的明显偏移，但是会对共振频率 中的单元进行独立设计并不是最优的选择。应该在

附近的STL造成一定的影响。 对组合结构设计的过程中充分考虑单元间的耦合
最后，还探究了单元顺序对组合结构STL 谱线 效应，并对其加以利用。例如，可以将共振频率相近
的影响。改变了 3 个单元的相对位置，同时固定单 的单元尽可能放置在相邻的位置处，以达到提升组
元间距L = 20 cm不变，基于FEM计算了不同顺序 合结构隔声效果的目的。

60 ፇ౞1-2-3 ፇ౞2 50 L=15 cm 50 1-2-3
ፇ౞1 ፇ౞3 L=20 cm 1-3-2
50 L=25 cm 2-1-3
40 40
STL/dB 30 STL/dB 30 STL/dB 30
40

20 20 20
10 10
10
0 0 0
200 300 400 500 200 300 400 500 200 300 400 500
ᮠဋ/Hz ᮠဋ/Hz ᮠဋ/Hz
(a) ӭ˔ӭЋˁጸՌፇ౞ᄊSTLࠫඋ (b) ӭЋᫎᡰࠫጸՌፇ౞STLᄊॖ־ (c) ӭЋᮋऀࠫጸՌፇ౞STLᄊॖ־

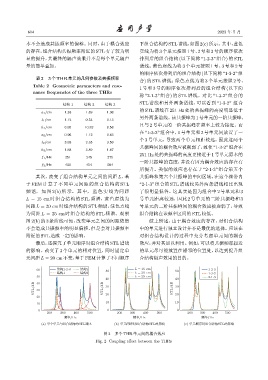
图 2 多个 THR 单元间的耦合效应
Fig. 2 Coupling effect between the THRs