Page 171 - 《应用声学》2023年第3期

第 42 卷 第 3 期 宋乐等： 相位失配弹性平板复合波导中的缺陷态
0.470
0.465
0.460
f/MHz
0.455
0.450
0.445
0 0.2 0.4 0.6
Dφ
图 9 不同缺陷态的频率随相位差变化
Fig. 9 Frequency of different defect states vs the [1] Ponge M F, Croënne C, Vasseur J O, et al. Control
phase difference
4 结论
本文设计了一种基于周期起伏结构的弹性平
板波导，并在波导结构中引入了相位失配产生的缺
陷，对透射谱禁带中产生的缺陷态特征进行了研究。
结论如下：
(1) 周期起伏弹性板中会形成弹性波禁带，引
入相位失配缺陷可以观察到禁带中的缺陷模透射
峰，且透射峰随相位差变化而发生频移。不仅如此，
禁带中透射峰的数目也受相位差大小影响。研究表
明边界起伏和相位连接条件都会影响弹性板的谱
带特性，不同的相位失配程度可以造成不同特征的
弹性波频谱，并且形成缺陷态的数目也不同。
(2) 对缺陷处的能量局域化现象进行了进一步
的分析，结果表明不同缺陷态的应力场以及空间位
移场分布具有不同的特征。研究表明，不同频率的
缺陷态对应的场分量存在不同的能量局域特征，分
别呈现出对称及反对称规律。
(3) 对于两种不同缺陷模式，归纳了相位差与
模式之间的频率分布，揭示了不同缺陷模式具有频
移周期不同的特征。
由于弹性波在波导内具有横波和纵波两种类
型，除了它们与结构的作用外，两者之间也存在相
互转换。所以即使结构中只引入一个相位失配缺
陷，禁带中也可能出现两个特性不同的透射峰。由
于产生缺陷态的频率与结构尺寸密切相关，等比例
放大结构参数，缺陷态频率也会随之降低。即便不
增大结构尺寸，目前的工艺也完全可以精确加工相
关的弹性薄板。进一步研制高精度的弹性波检测系
统，则可以对本文提出的相位失配缺陷态调控机理
609
进行实验验证。利用光学干涉方法高精度检测弹性
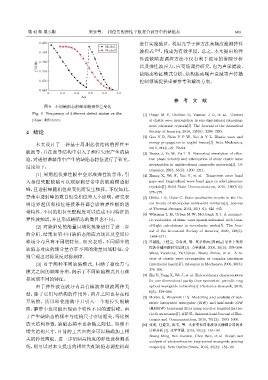
Mode1
Mode2 波模式 [19] ，将成为有效手段。总之，本文提出的弹
性波缺陷态调控方法不仅有利于波导的带隙分析
以及弹性波应力、应变场调控研究，也为声学滤波、
缺陷态特征模式分析、结构振动噪声衰减等声传播
控制领域提供重要参考和解决方案。
0.8 1.0
参 考 文 献
of elastic wave propagation in one-dimensional piezomag-
netic phononic crystals[J]. The Journal of the Acoustical
Society of America, 2016, 139(6): 3288–3295.
[2] Guo Y B, Shim V P W, Yeo A Y L. Elastic wave and
energy propagation in angled beams[J]. Acta Mechanica,
2010, 214(1–2): 79–94.
[3] Zhang J, Ye W, Yu T X. Numerical simulation of effec-
tive phase velocity and attenuation of shear elastic wave
propagation in unidirectional composite materials[J]. Ul-
trasonics, 2013, 53(6): 1200–1211.
[4] Zhang X, Wu F, Yao Y, et al. Transverse wave band
gaps and longitudinal wave band gaps in solid phononic
crystals[J]. Solid State Communications, 2010, 150(5–6):
275–279.
[5] Ghiba I D, Gales C. Some qualitative results in the lin-
ear theory of micropolar solid–solid mixtures[J]. Journal
of Thermal Stresses, 2013, 36(4–6): 426–445.
[6] Wiseman L M, Urban M W, McGough R J. A paramet-
ric evaluation of shear wave speeds estimated with time-
of-flight calculations in viscoelastic media[J]. The Jour-
nal of the Acoustical Society of America, 2020, 148(3):
1349–1371.
[7] 汪越胜, 于桂兰, 章梓茂, 等. 复杂界面 (界面层) 条件下的弹
性波传播问题研究综述 [J]. 力学进展, 2000, 30(3): 378–390.
Wang Yuesheng, Yu Guilan, Zhang Zimao, et al. A re-
view of elastic wave propagation at complex interfaces
(interfacial layers)[J]. Advances in Mechanics, 2000, 30(3):
378–390.
[8] Zhi Y, Yang X, Wu J, et al. Extraordinary characteristics
for one-dimensional parity-time-symmetric periodic ring
optical waveguide networks[J]. Photonics Research, 2018,
6(6): 579–586.
[9] Moitra S, Bhowmik P S. Modelling and analysis of sub-
strate integrated waveguide (SIW) and half-mode SIW
(HMSIW) band-pass filter using reactive longitudinal pe-
riodic structures[J]. AEUE - International Journal of Elec-
tronics and Communications, 2016, 70(12): 1593–1600.
[10] 张明, 任建文, 陈文, 等. 光折变长周期波导光栅耦合器的设
计和分析 [J]. 光学学报, 2015, 35(3): 153–161.
Zhang Ming, Ren Jianwen, Chen Wen, et al. Design and
analysis of photorefractive long-period waveguide grating
coupler[J]. Acta Optica Sinica, 2015, 35(3): 153–161.