Page 168 - 《应用声学》2023年第3期

606 2023 年 5 月

e e
d d

T
y T
x
К࠱ቫ W  ܿᦡᎥᬞ W  ѣ࠱ቫ ߹ᎿӜᦡࡏ
(50 mm) (50 mm) (30 mm)
图 1 弹性平板波导结构示意图
Fig. 1 Schematic diagram of the elastic plate waveguide structure

0.6 0.6

6 mm 0.5 0.5
v
u
f/MHz f/MHz
W  W  0.4 0.4
图 2 对接处的相位失配
Fig. 2 Phase mismatch at the junction 0.3 0.3
波在周期波导中传输时，由布拉格散射引起布
拉格共振则会导致频域禁带，并且布拉格共振频 0.2 0 0.2 0.2 -40 -20 0
率与周期长度有关 [16] 。根据Floquet定理与边界条 β/cm -1 T e /dB
(a) ᮠࣜፇ౞ (b) ᤩ࠱៨
件，可以得到频率f 与传播常数β 的关系式 [17] ：
v
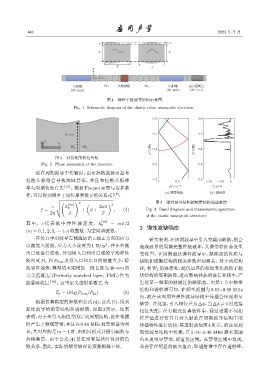
u( (m) ) 2 ( ) 2 图 3 弹性波导结构的频带结构和透射谱
c u k y 2nπ
f = t + β + , (4) Fig. 3 Band diagram and transmission spectrum
2π d T
of the elastic waveguide structure
(m)
其 中， c 代 表 板 中 弹 性 波 速 度， k y = mπ/2
2 弹性波缺陷态
(m = 0, 1, 2, 3, · · · )，n取整数，为空间谐波数。
在仿真中对波导左侧施加沿x轴正方向的应力 研究表明，在周期波导中引入变截面缺陷，则会
以激发入射波，应力大小设置为 1 N/m ，并在右侧 造成波导的周期完整性被破坏，其谱带特征会发生
2
出口处进行接收，分别用入口和出口域的平均弹性 变化 [8] 。在周期起伏弹性波导中，缺陷态的性质与

能密度 P In 和 P Out 表征入口和出口的能量大小，除 缺陷和周期结构的相关参数密切相关。对于两结构
波导区域外，模型的末端增加一段长度为30 mm 的 W 1 和W 2 的连接处，起伏边界的相位变化扰动了起
完美匹配层 (Perfectly matched layer, PML) 作为 伏结构的周期波数，进而影响共振的波长和频率，产
能量吸收层 [18] 。这里定义透射系数T e 为 生使某一频率的波通过的缺陷态。由第 1 节中频带
结构和透射谱可知，在频率范围为 0.44∼0.48 MHz
T e = 10 lg(P Out /P In ). (5)
内，波在该周期性弹性波导结构中传播会出现明显
根据仿真模型的参数和公式(4)、公式(5)，得到 禁带。在这里，引入相位差为∆ϕ，当∆ϕ ̸= 0时连接
弹性波导的频带结构和透射谱，如图 3 所示。结果 相位失配。在有限元仿真软件中，通过设置不同相
表明，对于未引入相位差的完美周期结构，波在传播 位差值进行仿真并对入射波在周期波导结构中的
时产生了频域禁带，并且在0.46 MHz处禁带最为明 传播特性进行比较，其透射谱如图4所示。波在该周
显，其对应的是m = 1时，由相同模式共振引起的布 期性波导结构中传播，在 0.44∼0.48 MHz 频率范围
拉格禁带。由于公式 (4) 是在没有起伏时得到的色 内出现明显禁带，即蓝色区域。在禁带区域中发现，
散关系，因此，实际的频带较理论预测稍稍下移。 总会存在明显的极大值点，即透射谱中存在透射峰。