Page 169 - 《应用声学》2023年第3期

第 42 卷 第 3 期 宋乐等： 相位失配弹性平板复合波导中的缺陷态 607

而且 ∆ϕ = 0 时，即连接相位匹配，呈现为完美周期 的应力场情况和弹性应变能密度分布进行数值模
结构，没有透射峰出现。这表明弹性波周期波导中， 拟，计算结果如图 5 和图 6 所示。结果表明，相位失
相位失配缺陷可以导致弹性波缺陷态。 配造成的缺陷处应力分布呈现出不同的局域化特
征。在这里，定义以缺陷处应力呈现极小值的缺陷
T e /dB
1.0 10
态为模式 1 (Mode 1)，而呈现极大值的缺陷态为模
0
0.8 式 2(Mode 2)。根据弹性波透射谱，在 ∆ϕ = 0.25
-10
时，Mode 1 对应频率 f 1 = 457.8 kHz，Mode 2 对
0.6 -20
Dφ 应频率为 f 2 = 467.9 kHz；在 ∆ϕ = 0.5 时，Mode 1
0.4 -30
-40 对应频率为 f 1 = 447.4 kHz，Mode 2 对应频率为
0.2 f 2 = 461.4 kHz。
-50
0 -60
0.44 0.45 0.46 0.47 0.48
/(NSm -2 )
f/MHz
(a) Dφ=0.25, Mode 1
图 4 透射谱随相位失配变化情况
3.0
Fig. 4 Transmission spectrum changes with the
2.5
phase mismatch (b) Dφ=0.25, Mode 2
2.0
可以看出，在归一化相位差从 0 到 1 的一个周 1.5
期内，损耗较高的蓝色区域中分布着 3 条透射率较 1.0
(c) Dφ=0.50, Mode 1
高的黄色曲线，对应着波导结构的禁带以及禁带中 0.5
的透射峰。随着相位差的变化，禁带中透射峰表现
出不同的频率值，即频移现象，说明通过相位差这一 (d) Dφ=0.50, Mode 2
结构参数可以实现对禁带中缺陷态的频率调控。
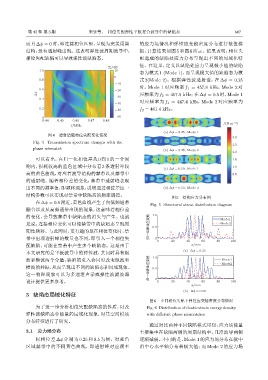
图 5 结构应力分布图
在∆ϕ = 0.6附近，黄色曲线产生了向低频通带
Fig. 5 Structural stress distribution diagram
融合以及从高频通带出现的现象，这意味着相位差
的变化，会导致禁带中缺陷态的消失与产生。也就 1.0 Mode1
是说，连接相位变化可以使禁带中的缺陷态呈现周 ॆʷӑुভऄԫᑟ 0.5 Mode2
期性频移。与此同时，更有趣的是在相位变化时，禁
带中出现透射峰的数量也不同，即引入一个相位失 0
0 20 40 60 80 100
配缺陷，可能在禁带中产生多个缺陷态。这是由于 x/mm
(a) Dφ=0.25
本文研究的是平板波导中的弹性波，其同时具有纵
波和横波两个分量，缺陷的引入会同时改变纵波和 1.0 Mode1
横波的共振，从而呈现出不同的缺陷态和局域现象。 ॆʷӑुভऄԫᑟ 0.5 20 40 60 80 Mode2
这一物理现象可以为多通道声学或弹性波滤波器
设计提供更多参考。 0 0 20 40 60 80 100
x/mm
(b) Dφ=0.50
3 缺陷态局域化特征
图 6 不同相位失配下弹性应变能密度分布情况
为了进一步分析相位失配缺陷态的性质，以及 Fig. 6 Distribution of elastic strain energy density
弹性波缺陷态中能量的局域化现象，对其空间模场 with different phase mismatches
分布特征进行了研究。
通过对比两种不同缺陷模式可知，应力场能量
3.1 应力场分布 主要集中在缺陷两侧的周期结构中，且沿波导两侧
以相位差 ∆ϕ 分别为 0.25 和 0.5 为例，对蓝色 逐渐减弱。不同的是，Mode 1 的应力场分布在板中
区域禁带中的不同黄色曲线，即透射峰对应频率 沿中心水平轴分布着极大值；而 Mode 2 的应力场