Page 116 - 《应用声学》2023年第4期
P. 116
778 2023 年 7 月
收水中的信号时,其正交归一性不是很好,但其他号 距离的声压矩阵 p(r, z),实验中声源深度为 55 cm
简正波为在水中传播的简正波,水中声场里其他号 时,不同深度水听器接收到的时域信号以及时频分
简正波的正交归一性都较好,通过KRAKENC计算 析结果如图9所示。
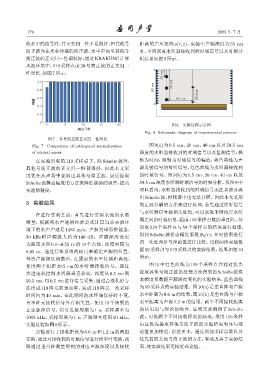
水池环境中,119 采样点前 20 号简正波的正交归一
10 cm
性对比,如图7所示。
1.0 55 cm
60 cm
0.8
0.6 60 cm 29.5cm
ࣨϙ
0.4
0.2
0
0 5 10 15 20 图 8 实验过程示意图
വগՂ
Fig. 8 Schematic diagram of experimental process
图 7 各号简正波正交归一性对比
Fig. 7 Comparison of orthogonal normalization 图 9(a) 为 0.5 cm、20 cm、40 cm 以及 59.5 cm
of normal waves 深度的水听器接收到的时域信号以及监测信号,横
在实验所取的 119 采样点下,除 Scholte 波外, 轴为时间,纵轴为时域信号的幅值,蓝色曲线为声
其他号简正波的正交归一性都很好,因此本文采 源发射信号的监听信号,红色曲线为水听器接收到
用优先从声场中提取出其他号简正波,最后提取 的时域信号。图 9(b) 为 0.5 cm、20 cm、40 cm 以及
Scholte波模态幅度的方法来降低实验的误差,提高 59.5 cm深度水听器时域信号的时频分析。从图9中
实验的精度。 可以看出,水听器接收到的时域信号无法直接分离
出Scholte波,时频谱中也无法分辨。因此本文采用
3 实验结果 简正波分解的方法来进行处理,首先通过监听信号
与水听器信号做相关处理,可以获取不同位置水听
在进行实验之前,首先进行实验水池的水温
器之间的时延信息,组成119采样点数的垂直阵。分
测量,根据纯水声速的经验公式计算当前实验环
别取 119 个采样点与 59 个采样点的结果进行处理,
境下的水声声速是 1485 m/s。声源为球形换能器,
得到 Scholte 波模态幅度系数 Φ 0 (r),并对结果进行
50 kHz 时声源级大约为 140 dB。声源深度设定
为距离水面 0.1∼0.55 m 的 10 个点位,深度间隔为 归一化处理后与理论值进行比较。比较两组实验数
0.05 m。通过行车系统的标尺来确定声源的位置。 据59采样点与119采样点的实验结果。结果如图10
每次声源深度调整后,在固定的水平传播距离处, 所示。
使用两个相距 29.5 cm 的水听器接收信号。通过 图 10 中红色曲线为 119 个采样点并通过优先
步进电机控制水听器垂直移动,深度从 0.5 cm 到 提取其他号简正波的处理方法得到的 Scholte 波模
59.5 cm,每 0.5 cm 进行信号采集,通过合成孔径方 态幅度系数随声源深度变化的实验结果,蓝色曲线
法组成 119 阵元的垂直阵,完成 119 阵元一次采样 为 59 采样点的实验结果。图 10(a) 是垂直阵与声源
时间约为 40 min,在此期间池水环境保持时不变, 水平距离为0.6 m 的结果,图10(b)是垂直阵与声源
首末阵元接收信号具有相关性。使用 10 个周期的 水平距离为声源 1.2 m 的结果。两个不同接收距离
正弦脉冲信号,信号发射周期为 1 s,采样频率为 的结果均与理论值吻合,证明实验测得了 Scholte
1000 kHz,采样周期为 1 s,声源频率使用 50 kHz。 波。对比两个不同接收距离的结果,采用 119 采样
实验过程如图8所示。 点且优先提取其他号简正波的实验结果明显与理
实验进行了接收距离为 0.6 m 和 1.2 m 的两组 论值更加接近,误差更小。通过增加采样点数以及
实验,通过对接收到的时域信号进行傅里叶变换,获 优先提取其他号简正波的方法,有效改善了实验结
取通过垂直阵测量得到的对应声源深度以及接收 果,使实验结果更接近理论值。