Page 77 - 《应用声学》2023年第4期

第 42 卷 第 4 期 刘婉婷等： 螺旋型电磁超声辐射声场对缺陷检测影响的计算机模拟 739

1.2 静磁场与动磁场的分析
භᇓᨡ
ጳڔ
O r out 利用有限元模型可以计算得到 EMAT 模型中
តನ r in 的静磁场与动磁场分布。图 3 是静磁场的磁感应强
n h
度沿r 向的分布。动磁场是施加交变电流时产生的，
并在工件内产生涡流。当施加的激励电流的频率为
(a) ᛃ஽یEMATፇ౞ᇨਓڏ (b) ጳڔፇ౞ᇨਓڏ 1 MHz、幅度为50 A时得到的涡流密度幅度随距离
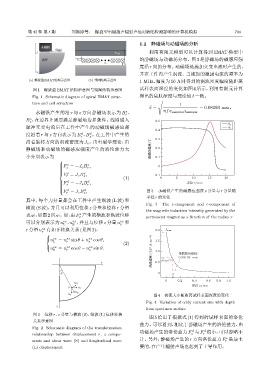
图 1 螺旋型 EMAT 结构示意图与线圈结构示意图 试样表面深度的变化如图 4 所示，利用有限元计算
Fig. 1 Schematic diagram of spiral EMAT struc- 得出的集肤深度与理论值δ 一致。
√
ture and coil structure 1
δ = = 0.08193 mm。
永磁铁产生的沿 r 与 z 方向静磁场表示为 B 、 πfσ sample µ sample
s
r
s
B ，在边界上需要满足静磁场边界条件。线圈通入
z 0.5
B z
脉冲交变电流后在工件中产生的动磁场磁感应强 B r
0.4
度沿着 r 与 z 方向表示为 B 、B 。在工件中产生的
d
d
r
z
0.3
沿着旋转方向的涡流密度为 J e 。由电磁学理论，由
静磁场和动磁场的磁感应强度产生的洛伦兹力大 ᇓਖऄूए/T 0.2
小分别表示为 0.1

s
s
F = −J e B , 0

 z r


 s s
 F = J e B , -0.1
r z
(1) 0 5 10 15 20
d
d
F = −J e B , ӧय़ r/mm

 z r


 d d
 F = J e B , 图 3 永磁铁产生的磁感应强度 z 分量与 r 分量随
z
r
半径 r 的变化
其中，每个力分量都会在工件中产生纵波 (L 波) 和
Fig. 3 The z-component and r-component of
横波 (S 波)，并且可以利用位移 z 分量和位移 r 分量
the magnetic induction intensity generated by the
表示，如图2所示。如，由F 产生的横波和纵波位移 permanent magnet as a function of the radius r
s
z
sz
sz
可以分别表示为 u 、u ，并且与位移 z 分量 u 和
sz
S
L
z
sz
r 分量u 有如下转换关系(见图2)： 2.0
r J max

 sz sz sz
u L = u r sin θ + u z cos θ, 1.5
(2)
 sz sz sz
u S = u r cos θ − u z sin θ. ๤ืूए/(10 7 ASm -2 ) 1.0 ᬷᐩ஍ऄງए:
r 0.5 J max/e 0.08192 mm
θ 0
0 0.2 0.4 0.6 0.8 1.0
u S
Ԓए z/mm
P u r
u L
图 4
u z 涡流大小随距离试样表面深度的变化
Fig. 4 Variation of eddy current size with depth
z
from specimen surface
图 2 位移 r、z 分量与横波 (S)、纵波 (L) 位移转换
图 5 给出了根据式 (1) 得到的试样表面的洛伦
关系示意图
兹力。可以看到，相比于静磁场产生的洛伦兹力，由
Fig. 2 Schematic diagram of the transformation
d
d
动磁场产生的洛伦兹力 F 与 F 很小，可以忽略不
relationship between displacement r, z compo- z r
s
nents and shear wave (S) and longitudinal wave 计。另外，静磁场产生的 r 方向洛伦兹力 F 是最主
r
(L) displacement 要的，在产生辐射声场也起到了主导作用。