Page 80 - 《应用声学》2023年第4期

742 2023 年 7 月

 2 √ 2
2
4κ cos θ κ − sin θ
 r
 ,
L
M (θ) = ( √
 ) 2
κ − 2 sin θ + 2 sin θ sin 2θ κ − sin θ
 2 2 2 2
(6)
 2κ cos 2θ
 r
M (θ) = √ ,

 S ( 2 ) 2 2 2
κ 1 − 2 sin θ + 2 sin θ sin 2θ 1 − κ sin θ
其中，κ为纵波与剪切波波数比，κ = k P /k S 。 横波的远场半空间指向性函数为
可以看到，公式(5)相当于对力源f(R , ω)进行 hf
′
H (e R , θ, ω)
S
空间傅里叶变换。因此，求解洛伦兹力产生的声束 1 ∫∫∫
′
′
= M S (θ) f(R , ω) · e θ e −jk S R ·e R 3 ′
d R
指向性之前，需要对力源进行空间傅里叶变换。 4πc S Z S
cos θ
˜ s
= − M S (θ)F (θ), (7)
r
2.2 表面等效洛伦兹力的空间傅里叶变换 4πc S Z S
洛伦兹力的计算，需要得到永磁铁的磁感应 其中：
∫
a
s
强度和涡流的强度。在理论上可以借助 Dodd & F (θ) = F jJ (k S sin θr)rdr,
˜ s
1
r
r
0
Deeds 模型得到解析的结果 [7] ，或者利用 Tree方法
J 1 为一阶第一类贝塞尔函数。
得到级数解 [5] 。但是这两种方法在具体操作过程中
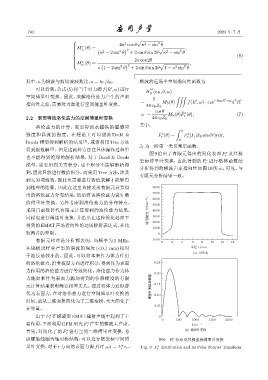
图 9 给出了有限元得出的简化表面 F 及其极
s
r
也不能得到绝对的解析结果，对于 Dood & Deeds
s
坐标傅里叶变换，由此得到的 F 进行格林函数法
模型，需要用到无穷积分，这个积分不能够解析得 r
分析得到的横波声束指向性如图 10 所示，可见，与
到，因此只能进行数值积分。而采用Tree 方法，涉及
有限元分析结果一致。
到无穷项级数，因此也需要进行数值求解才能够得
到相应的结果。因此在这里直接采用有限元计算得 8000
出的洛伦兹力分布结果，然后将该洛伦兹力进行数 7000
值傅里叶变换。另外考虑到洛伦兹力的分布特点， 6000
5000
采用门函数替代有限元计算得到的洛伦兹力结果， ว͠ᇓҧ/(NSm -2 ) 4000
同样也进行傅里叶变换，并给出在这种简化处理下 3000
得到的 EMAT声场指向性的远场解析表达式，并比 2000
1000
较两者的差别。 0
有限元和理论分析都表明，当频率为 1 MHz， -1000 0 2 4 6 8 10 12 14
在铝板试样中产生的涡流的深度 (<0.1 mm) 相对 ӧय़ r/mm
(a) F r Ѭ࣋
s
于波长是较小的。因此，可以将本来作为体力作用
的洛伦兹力，沿着板厚方向进行积分，得到作为表面 0.25
力作用的洛伦兹力进行等效简化。洛伦兹力作为体
0.20
力施加和作为表面力施加得到的位移幅度的有限
元计算结果表明两者相差无几。通过将体力近似替 Ϭ᧗Ձԫ૱Ցࣨϙ 0.15
代为表面力，在对洛伦兹力进行空间傅里叶变换的 0.10
时候，就从三维变换简化为了二维变换，大大简化了
0.05
计算量。
s
由于 F 在螺旋型 EMAT辐射声场中起到了主 0
r
0 500 1000 1500 2000
要作用，下面利用GFM研究F 产生的横波主声束。 k/m -1
s
r
首先，对简化了的 F 进行空间二维傅里叶变换，考 (b) Ϭ᧗Ձԫ૱
s
r
虑螺旋线圈为轴对称结构，可以进行极坐标空间傅 图 9 F r 分布及其极坐标傅里叶变换
s
s
里叶变换，对于 r 方向的表面力源 f(R , ω) = F e r ， Fig. 9 F r distribution and its Polar Fourier Transform
′
s
r