Page 81 - 《应用声学》2023年第4期

第 42 卷 第 4 期 刘婉婷等： 螺旋型电磁超声辐射声场对缺陷检测影响的计算机模拟 743

0O 算得到的声束指向性，可以看到SGFM 与其他两种
330O 30O
方法求解结果一致性很好。
300O 60O
8000
7000
GFM
FEM
270O 90O 6000
图 10 GFM 和 FEM 计算得到的横波声束指向性 ᛫᭧ว͠ᇓҧ/(NSm -2 ) 5000
4000
对比 3000
Fig. 10 Comparison of shear wave beam directiv- 2000
ity calculated by GFM and FEM calculations 1000
0
2.3 格林函数简化解析结果
-1000
0 2 4 6 8 10 12 14
在利用格林函数法分析横波辐射声场过程中，
ӧय़ r/mm
s
可以看到，实际上洛伦兹力 F 分布与门函数十分 (a) እӑว͠Шҧ
r
相似，因此可以考虑用门函数表达式替代有限元结
0.25
果得到的洛伦兹力分布，从而得到简化的格林函数 దᬍЋᝠካፇ౧
እӑവیᝠካፇ౧
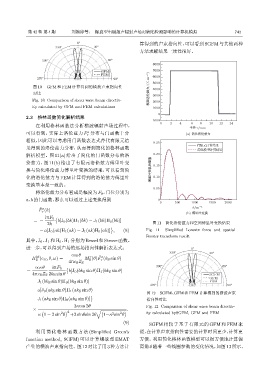
解析模型。图 11(a) 给出了简化的门函数分布的洛 0.20
伦兹力，图 11(b) 给出了有限元洛伦兹力傅里叶变 0.15
换与简化洛伦兹力傅里叶变换的结果，可以看到简 Ϭ᧗Ձԫ૱Ցࣨϙ
化的洛伦兹力与 FEM 计算得到的洛伦兹力傅里叶 0.10
变换基本是一致的。
0.05
将洛伦兹力分布看成是幅度为 F 0 ，门位分别为
a、b的门函数，那么可以通过上述变换得到 0
0 500 1000 1500 2000
-1
k/m
˜ s
F (k) (b) Ϭ᧗Ձԫ૱
r
iπF 0 {
= − b[J 0 (bk)H 1 (bk) − J 1 (bk)H 0 (bk)]
2k 图 11 简化洛伦兹力和空间傅里叶变换结果
}
− a[J 0 (ak)H 1 (ak) − J 1 (ak)H 0 (ak)] , (8) Fig. 11 Simplified Lorentz force and spatial
Fourier transform result
其中，J 0 、J 1 和 H 0 、H 1 分别为 Bessel 和Struve 函数。
进一步，可以得到声场的远场指向性解析表达式： 0O
330O 30O
cos θ
hf r ˜ s
H (e R , θ, ω) = − M (θ)F (k S sin θ)
S
S
r
4πc S Z S
cos θ iπF 0 { 300O 60O
= b[J 0 (bk S sin θ)H 1 (bk S sin θ)
4πc S Z S 2k S sin θ SGFM
GFM
− J 1 (bk S sin θ)H 0 (bk S sin θ)] FEM
270O 90O
− a[J 0 (ak S sin θ)H 1 (ak S sin θ)
图 12 SGFM、GFM 和 FEM 计算得到的横波声束
}
− J 1 (ak S sin θ)H 0 (ak S sin θ)] 指向性对比
2κcos 2θ Fig. 12 Comparison of shear wave beam directiv-
× √ .
( 2 ) 2 ( 2 ) ity calculated bySGFM, GFM and FEM
2
κ 1 − 2 sin θ +2 sinθsin 2θ 1−κ sin θ
(9) SGFM 相较于基于有限元的 GFM 和 FEM 来
利用简化格林函数方法 (Simplified Green’s 说，在计算声束指向性需要的计算时间更少，计算更
function method, SGFM) 可以计算螺旋型 EMAT 方便。利用简化格林函数模型可以很方便地计算偏
产生的横波声束指向性。图12对比了用3 种方法计 离角θ 随着一些线圈参数的变化情况，如图13所示。