Page 153 - 《应用声学）》2023年第5期

第 42 卷 第 5 期 杨昱皞等： 时频特征的海豚发声端点检测方法研究 1045

均幅度是一帧声信号的幅度大小的表征，短时能量 click 信号最高可以达到 100 ∼ 150 kHz，改进后的
通过对信号振幅平方，将振幅的变化扩大，因此短时 公式为
能量更能够体现出信号的变化；短时自相关系数是 ∑ N 1 ∑ N 2
F k 1 X k 1 F k 2 X k 2
衡量信号自身波形在时域上变化程度的指标，但是 C i = Q 1 ∑ N 1 + Q 2 ∑ N 2 , (7)
k 1
k 2
海洋环境噪声场的构成很复杂，由于信号的无序性， X k 1 X k 2
k 1 k 2
短时自相关系数不适用处理海洋环境声音。因此选
式 (7) 中，Q 1 是海豚声音频率范围的权重；Q 2 是非
择短时能量作为参数，可以增大目标声信号和噪声
海豚声音频率范围的权重；N 1 是海豚声音频率范
之间的区分度，计算公式 [19] 如下：
围；N 2 是非海豚声音频率范围。由于海洋环境噪声
N
∑ 2 场的低频能量很大，海豚声音对谱质心的提升不明
E i = x (m), (3)
n 显，为了能够更好地区分海豚发声的声段，设定海豚
m=1
声音频率范围的权重应当大于非海豚声音频率范
式 (3) 中，E i 是第 i 帧的短时能量，N 是单帧信号的
围的权重。同时由于海豚的click信号和burst-pulse
采样点数，m是采样点序号，x n (m)是每一个采样点
信号是宽频信号，所以不能不考虑非海豚声音频率
的振幅大小。海洋环境中的噪声大多比较平稳，能
范围的分量。由于本文中使用的实验数据较为纯
量波动范围不大，当出现目标声信号时，该时刻短时
净，低频噪声的能量不大，因此拟定Q 1 为0.6，Q 2 为
能量会增大，通过短时能量和持续时间可以一定程
0.4。在不同的环境或者数据中，Q 1 、Q 2 的值应做适
度区分目标声音。
当修改。
1.3.3 频域分析 为了找到目标发声的起始点和终止点，引入谱
对声音进行傅里叶变换，计算公式 [6] 如下： 质心一阶偏移率，即每一帧谱质心相对于上一帧谱

∞ 质心的变化。谱质心二阶偏移率，即谱质心变化的
∑
X l = x n e −jωt . (4)
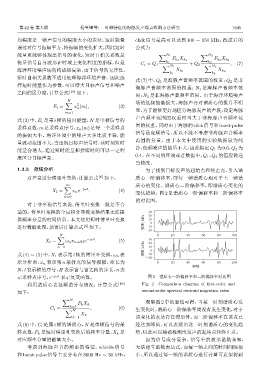
变化趋势。图 2 是谱质心一阶偏移率和二阶偏移率
n=0
的对比图。
对于非平稳信号来说，傅里叶变换一般是不合
适的。傅里叶变换的全局积分导致变换结果无法提 30
20
供频率分量的时间信息。本文使用短时傅里叶变换 ᮠဋ/kHz 10 0
进行数据处理，加窗后计算公式 [6] 如下： -10
-20
N 0 20 40 60 80 100
∑ −jωt
X l = ω n x n+lH e . (5) 30
20
n=0 ᮠဋ/kHz 10 0
式 (4) ∼ (5) 中，X 1 表示第 l 帧的傅里叶变换，ω n 表 -10
-20
示分析窗，x n 表示第 n 采样点的信号振幅，窗长为 0 20 40 60 80 100
ࣝ஝
N，l 表示帧的序号，H 表示窗与窗之间的步长，n 表
示采样点序号，e −jωt 表示复变函数。 图 2 谱质心一阶偏移率和二阶偏移率对比图
利用谱质心表征频谱分布情况，计算公式 [19] Fig. 2 Comparison diagram of first-order and
如下： second-order spectral centroid migration rates
∑ N
观察图 2 中的竖线可得，当某一时刻谱质心发
F k X k
C i = k=1 , (6) 生变化时，谱质心一阶偏移率尚没有发生变化，对于
∑ N
X k
k=1 该变化的表达存在滞后性，而二阶偏移率在该点已
式 (6) 中，C i 是第 i 帧的谱质心，N 是单帧信号的采 经达到峰值，可以表现出这一时刻谱质心的变化趋
样点数，F k 是短时傅里叶变换后的频率分量，X k 是 势，以此可以精确检测出发声的起始点和终止点。
对应频率分量的能量大小。 因为信号成分复杂、信号中的波形函数未知，
考虑到海豚声音的频率的特征，whistle 信号 无法建立函数表达式，而每一帧之间的时间间隔很
和 burst-pulse 信号主要分布在 8000 Hz ∼ 30 kHz， 小，所以通过每一帧的谱质心进行计算可近似得到