Page 154 - 《应用声学）》2023年第5期

1046 2023 年 9 月

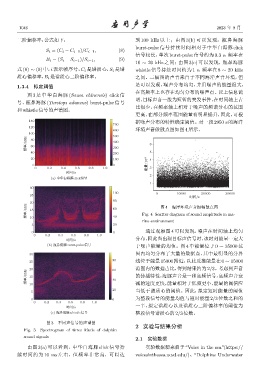
二阶偏移率，公式如下： 到 100 kHz 以上；由图 3(b) 可以发现，瓶鼻海豚
burst-pulse 信号持续时间相对于中华白海豚 click
S i = (C i − C i−1 )/C i−1 , (8)
信号较长，单次 burst-pulse 信号约为 0.3 s，频率在
B i = (S i − S i−1 )/S i−1 , (9)
10 ∼ 20 kHz 之间；由图 3(c) 可以发现，瓶鼻海豚
式 (8) ∼ (9) 中，i 表示帧序号，C i 是谱质心，S i 是谱 whistle 信号持续时间约为 1 s，频率在 8 ∼ 20 kHz
质心偏移率，B i 是谱质心二阶偏移率。 之间。三幅图的声音来自于不同海洋声音环境，但

1.3.4 拟定阈值 是可以发现，噪声分布均匀，并且噪声的能量很大，
在高频率上也存在均匀分布的噪声点。以上信息说
图 3 是中华白海豚 (Sousa chinensis) click 信
明，目标声音一般为短暂的突发事件，在时间轴上占
号、瓶鼻海豚 (Tursiops aduncus) burst-pulse 信号
比很少，在频率轴上相对于噪声的频谱分布的范围
和whistle信号的声谱图。
更高，在部分频率范围能量有明显提升，因此，可根
140 据噪声分布的特性确定阈值。对一段2950 s的海洋
700
120
600 环境声音做散点图如图4所示。
100
500
ᮠဋ/kHz 60 400 6
80
300
40 200 5
20 100 4
0 0 ᑟ᧚/10 4
0 0.2 0.4 0.6 0.8 1.0 3
௑ᫎ/s
2
(a) ˗Өᄇ๒៵clickηՂ
1
30
100 0 10000 20000 30000
25
௑ᫎ/s
80
20
ᮠဋ/kHz 15 60 Fig. 4 Scatter diagram of sound amplitude in ma-
海洋环境声音振幅散点图
图 4
40
10
rine environment
5 20
0 0 通过观察图 4 可以发现，噪声在时间轴上均匀
0 0.2 0.4 0.6 0.8 1.0
௑ᫎ/s 分布，因此当出现目标声信号时，该时刻能量一定大
(b) ၫᴋ๒៵burst-pulseηՂ 于噪声能量的均值。图 4 中能量位于 0 ∼ 35000 范
30 围内均匀分布了大量的数据点，其中最明显的分界
80
25 线位于能量 15000附近，以此反推能量在0 ∼ 15000
20 60 范围内的数据占比，得到结果约为2/3。考虑到声音
ᮠဋ/kHz 15 40 的传播特性，海豚声音是一种高频信号，高频声音衰
减的速度更快，能量相对于低频更小，能量的阈值应
10
20 当低于谱质心的阈值。因此，拟定短时能量的阈值
5
0 0 为整段信号的能量均值与短时能量 2/3位数之和的
0 0.2 0.4 0.6 0.8 1.0
௑ᫎ/s 一半，拟定谱质心以及谱质心二阶偏移率的阈值为
(c) ၫᴋ๒៵whistleηՂ 整段信号谱质心的2/3位数。

图 3 不同声信号的声谱图
2 实验与结果分析
Fig. 3 Spectrogram of three kinds of dolphin
sound signals
2.1 实验数据
由图 3(a) 可以看到，中华白海豚 click 信号持 实验数据源来自于“Voice in the sea”(https://
续时间约为 10 ms 左右，但频率非常高，可以达 voicesinthesea.ucsd.edu/)、“Dolphins Underwater