Page 33 - 《应用声学)》2023年第5期
P. 33
第 42 卷 第 5 期 郭同政等: 反射波测井的菲涅尔带效应 925
用黑色实线表示,实轴积分 (Real axial integration, 横波波长的 1/5。当弹性波遇到裂缝 1 时,会发生绕
RAI) 结果用红色实线表示。从图中可以看出,两种 射现象,弹性波会绕过裂缝1,继续向裂缝2传播,因
算法得到的波形在到时与幅度上基本吻合,斯通利 此从波场快照图中几乎看不到反射波的存在。
波的幅度略有差异,这些差异主要受到用直角坐标 在井中布置多极子接收器,井轴附近周向布置
系阶梯型网格来模拟圆形井孔所造成的误差,以及 4 个接收单元记录声压信号,对多极子接收器对角
网格尺寸大小、差分格式精度等的影响,减小网格 单元的数据进行相减,可以得到相应方向的偶极
尺寸,用更多的网格来描述井孔,有望得到更准确的 子数据。图 2(c) 为 Y Y 分量 (Y 方向偶极子源激发,
模拟效果。
Z
ᜈᎋ
2 反射波测井的有限差分模拟 Y 0.1 m
3.0 m
表 1 是模拟用的主要参数。图 2(a) 是井外 7 m 7 m
左右范围内两充液裂缝的模拟实例。模型大小为
x = 9.5 m、y = 3 m、z = 10 m,井孔半径为 10 m
0.1 m。采用非均匀网格,在井孔附近网格大小为 Y
∆x = ∆y = 0.01 m、∆z = 0.02 m,裂缝附近网格
X
大小为∆x = 0.001 m、∆y = 0.01 m、∆z = 0.02 m,
地层中网格为 ∆x = ∆y = ∆z = 0.02 m,时间步 (a) വલی
长 0.15 µs,地层参数见表 1。两个裂缝厚度均取
ࠕए/m
0.004 m,裂缝走向方向展布 (即 Y 方向长度) 均为 1 2 3 4 5 6 7 8 9
ᜈᎋ1 ᜈᎋ2
0.1 m,两个裂缝间隔 1.2 m。偶极声源指向为 Y 方
向,与裂缝走向平行,此时得到的反射波为SH横波, 2 ̌˗ܦູᣣ࠱ᄊुভฉ
不包含其他转换波。声源中心频率为3.5 kHz。
4
表 1 模型参数设置
Table 1 Parameters of the computation model ງए/m
6 ᜈᎋ1ᄊԦ࠱ฉ
ౝॲी
纵波速度 横波速度 密度
Medium
/(m·s −1 ) /(m·s −1 ) /(kg·m −3 ) 8
井孔流体 1500 0 1000 ̌ߘ
裂缝内流体 1500 0 1000
10
地层 3000 1800 2000 (b) 5 msฉڤঌི
根据固体中的弹性波理论,对于远探测声波测 5.0
井而言,波在介质中传播遇到异常体时,根据波长与
异常体尺度的相对大小,可产生反射波 (波长远小 4.5
于界面尺度,如地层界面)、散射波(波长和界面尺度
相当,如裂缝和溶洞等) 和绕射波 (波长远大于异常 ູᡰ/m 4.0
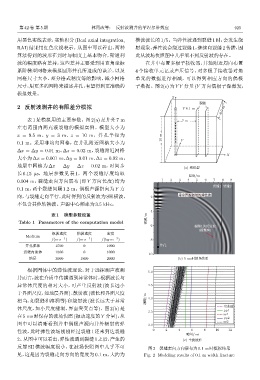
体尺度,如小尺度缝洞、界面突变点等)。图 2(b) 是 िజฉ
3.5 pp1
在5 ms时保存的波场快照(振动速度的Y 分量),从 ss1
pp2
图中可以清晰看到井中偶极声源向井外辐射的弹 3.0 ss2
性波,此时弹性波场刚刚经过裂缝 1 还未到达裂缝 0 2 4 6 8 10 12
ᫎ/ms
2。从图中可以看出,弹性波遇到裂缝1之后,产生的 (c) Лฉฉॎ
反射 SH 横波幅度很小,在波场快照图中几乎不可 图 2 裂缝走向方向展布为 0.1 m 时模拟结果
见,这是因为裂缝走向方向的宽度为 0.1 m,大约为 Fig. 2 Modeling results of 0.1 m width fracture