Page 28 - 《应用声学）》2023年第5期

920 2023 年 9 月

补偿 (温升补偿步进量为 0.01 Hz) 后，实际步进量 可调。
为 1 Hz；当判定电流与电压相位差变化较小时
U o = DU in , (3)
(ε 2 /2 > ε > ε 1 /2)，温升补偿起主要作用，负载追频
D = 2T on /T. (4)
已补偿的叠加量保持不变，其追频逻辑如图 4 所示，
移相调节量的大小由 DDS 控制原理中的相位
其中f r 为实时驱动频率，f i 为起始谐振频率。
控制字 P 决定，考虑到死区及续流，取最大占空比
᠇ᣒԫӑᤝᮠनݽ
为0.8。实时相位控制字P r 如式(5)所示：

P r = P i + ∆P 步进 ,
f r=f i-Df ພӤ+Df ᠇ᣒԫӑ (5)
Df ພӤ=Df ພӤ+0.01 其 中，P i 为 起 始 占 空 比 D i 对 应 的 相 位 控 制 字，
∆P 步进 为功率调节时对应的相位控制字。
Df ᠇ᣒԫӑ=Df ᠇ᣒԫӑ +1.01
3.2.2 输入电流与焊接振幅关系研究
N
ᄱͯࣀ Ĺε  /2? 根据式 (6) 可知，超声电源内阻 r 一定的情况
下，换能器的动态支路的阻抗变化与输入电流I in 存
Y
在对应关系，控制输入电流 I in 的大小，即可实现对
N
ᄱͯࣀ Ĺε  /2?
动态支路电流的调节：
Y U in
I in = 2 , (6)
N r + R 1 /[1 + (ω s C 0 R 1 ) ]
ཝଌፇౌ
式 (6) 中，R 1 为换能器的动态电阻，C 0 为换能器的
Y
静态电容，ω s 为换能器的串联谐振角频率。
᠇ᣒԫӑᤝᮠፇౌ
为进一步研究输入电流与焊接振幅的关系，分
图 4 负载变化追频逻辑 别以占空比 0.55、0.60、0.65、0.70、0.75 及 0.80 对铜
Fig. 4 Load change chasing logic 片进行焊接，铜片焊接参数同表 1。使用激光测振
根据 DDS 调频原理可知，当 FPGA 系统时钟 仪 OptoGUI 和功率计 PW9800 记录最大焊接振幅
f clk 和相位累加器数字 N 确定后，输出频率 f out 值 和最大输入电流。
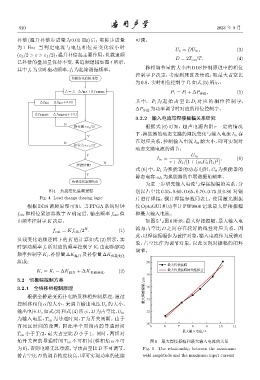
由频率控制字K 决定： 如图 5 与图 6 所示，最大焊接振幅、最大输入电
N
f out = Kf clk /2 . (1) 流与占空比 D 之间存在较好的线性对应关系。因
此，以焊接振幅作为被控对象，输入电流作为反馈对
负载变化追频逻辑下的 K 值计算如式 (2) 所示，实
象，占空比作为调节对象，以此实现对振幅的闭环
时驱动频率 f r 所对应的频率控制字 K r 由起始驱动
调节。
频率控制字 K i 、补偿量 ∆K 温升 及补偿量 ∆K 负载变化
组成： 20
తܸཝଌ૝ࣨ
K r = K i − ∆K 温升 + ∆K 负载变化 . (2) తܸཝଌ૝ࣨᄊጳভલՌ
18
3.2 恒振幅控制方案

3.2.1 全桥移相控制原理 తܸཝଌ૝ࣨ/mm 16
根据全桥逆变拓扑电路及移相控制原理，通过 14
控制移相角 α 的大小，来调节输出电压 U o 的大小。
输出电压U o 如式(3)和式(4)所示，D 为占空比，U in 12
为输入电压，T on 为导通时间，T 为开关周期。由于
有死区时间的设置，因此半个周期内的导通时间 10 5 6 7 8 9 10 11
T on 小于 T/2，最大占空比 D 小于 1。同时，两组对 తܸᣥКႃื/A
角开关管的导通时间 T on 不可相同 (移相角 α 不可 图 5 最大焊接振幅和最大输入电流的关系
为 0)，否则电路无法续流，导致占空比 D 不可调节。 Fig. 5 The relationship between the maximum
若占空比 D 的调节精度较高，即可实现功率的连续 weld amplitude and the maximum input current