Page 186 - 《应用声学》2024年第1期

182 2024 年 1 月

(11.2 mm和12 mm)和辐照时间即加热时间(5 ms、
0.2 10 ms 和 20 ms) 等，研究各参数对声场和温度场的
影响。
参照文献 [14,25] 的方法来比较不同功率下线
ࣨϙ/MPa 0 性与非线性声压及温度的差异。使用t检验方法，显

著性水平为 0.05，当 p > 0.05 时认为线性与非线性
-0.2 模型之间的差别无统计学意义。相反，当 p < 0.05
时说明两种模型之间具有差异，需要考虑非线性效
0 0.2 0.4 0.6 0.8 1.0
௑ᫎ/ms 应的影响。

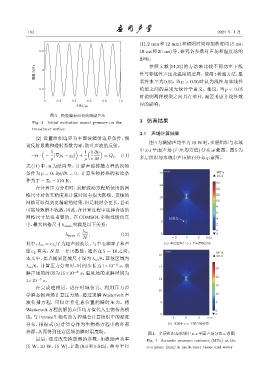
图 3 换能器表面初始激励声压
3 仿真结果
Fig. 3 Initial excitation sound pressure on the
transducer surface
3.1 声场计算结果
(2) 设置组织边界为平面波辐射边界条件，假
图4为激励声功率为10 W时，多层组织与水域
设反射系数和透射系数为零，防止声波的反射。
中 x-z 平面声场 (声压均方值) 分布示意图。图 5 为
1 1 1 ∂p
( ) ( )
−n · − (∇p t − q d ) + = Q i , (11) 多层组织与水域中声压轴向分布示意图。
ρ ρ c ∂t
式 (11) 中，n 为法向量。计算声波传播方程的初始
条件为 p = 0，∂p/∂t = 0。计算生物传热的初始条 16 mm MPa
16.4
件为T = T 0 = 310 K。 16
14
在计算压力分布时，求解波动方程所使用的网 14
格尺寸对仿真精度和计算时间有很大影响。更细的 12
12
网格可以得到更精确的结果，但是耗时会更长，甚至 10
8
可能导致解不收敛，因此，在计算过程中选择合适的 10
6
网格尺寸是很重要的。在 COMSOL 多物理场仿真 Ԧ࠱ག 4
8
中，最大网格尺寸h max 应满足以下关系： 2
0
h max 6 λ w , (12) 6 0
N -2 0 2 mm
其中，λ w = c L /f 为超声波波长，与中心频率 f 和声 (a) ܳࡏጸጻ˗ x-z ࣱ᭧ܦڤѬ࣋
速 c L 有关，N 是一个正整数，通常在 5 ∼ 10 之间。 mm MPa
16 28.6
本文中，焦点椭圆区域尺寸设为 λ w /8，其他区域为
λ w /6。计算压力分布时，时间步长为 1×10 −9 s，求 14
25
解声场的时间为 15×10 −6 s；温度场的求解时间为
20
12
1×10 −5 s。
15
在完成建模后，进行时域仿真。利用压力声
10
学瞬态物理场计算压力场，通过求解 Westervelt 声 10
波传播方程，可以计算任意位置的瞬时压力。将 8 5
Westervelt 方程的解的声压均方值代入生物传热模 0
6 0
块，与Pennes生物传热方程耦合计算组织中的温度 -2 0 2 mm
分布，根据式 (5) 计算 Q 作为生物热方程中的外部 (b) ඵ۫˗ x-z ࣱ᭧ܦڤѬ࣋
热源，从而得到任意区域的瞬时温度场。 图 4 多层组织与水域中 x-z 平面声场分布示意图
最后，通过改变换能器的参数，如激励声功率 Fig. 4 Acoustic pressure contours (MPa) at the
(5 W、10 W、15 W)、F 数 (0.6 和 0.645)、曲率半径 x–z plane (mm) in multi-layer tissue and water