Page 187 - 《应用声学》2024年第1期

第 43 卷 第 1 期 徐慧等： 高频聚焦超声声场和温度场的仿真研究 183

由结果可知，在多层组织中大部分声能聚焦在 声压计算声压增长百分比。
长约 0.638 mm、宽约 0.2 mm 的椭圆形聚焦区。在
皮下脂肪层 (焦点区域) 声压达到最大值 16.4 MPa。 30
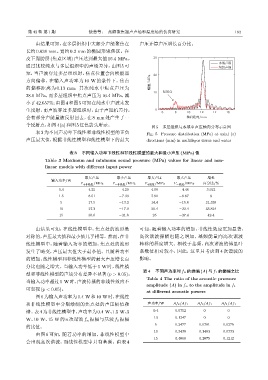
ඵ۫ܦڤ
通过比较纯水与多层组织中的声场差异，由图 5 可 ጸጻܦڤ
知，当声波穿过多层组织时，焦点位置会向换能器 20
方向偏移，在输入声功率为 10 W 的条件下，焦点 ࣨϙ/MPa
的偏移距离为 0.13 mm；其次纯水中焦点声压为
10 Ԧ࠱ག
28.6 MPa，而多层组织中焦点声压为 16.4 MPa，减
小了 42.657%；由图4 和图5 可知在纯水中声波未发
生反射，而声波穿过多层组织时，由于声阻抗差异， 0 6 8 10 12 14 16
会有部分声能量被反射回去，在 8 mm 处产生了一 ᣉՔᡰሏ/mm
个反射点，如图4(a)和图5红色箭头所示。
图 5 多层组织与水域中声压轴向分布示意图
表3 为不同声功率下线性和非线性模型的正负 Fig. 5 Pressure distribution (MPa) at axial (z)
声压最大值，根据非线性模型和线性模型下的最大 directions (mm) in multilayer tissue and water

表 3 不同输入功率下线性和非线性模型的最大和最小声压 (MPa) 值
Table 3 Maximum and minimum sound pressure (MPa) values for linear and non-
linear models with different input power

最大声压 最小声压 最大声压 最大声压 增长
输入功率/W
P +非线性 /MPa P −非线性 /MPa P +线性 /MPa P −线性 /MPa 百分比/%
0.4 4.25 −4.29 4.09 −4.48 3.912
1.5 8.51 −7.39 7.91 −8.67 8
5 17.5 −13.2 14.4 −15.8 21.528
10 27.3 −17.9 20.4 −22.4 33.824
15 35.6 −21.8 25 −27.4 42.4

由结果可知，在线性模型中，焦点处的波形是 可知，随着输入功率的增加，非线性效应更加显著，
对称的，声压最大值和最小值几乎相等。然而，在非 高次谐波振幅也随之增加，基频能量向高次谐波
线性模型中，随着输入功率的增加，焦点处的波形 转移的程度增大。相较于基频，高次谐波的傅里叶
发生了畸变，声压最大值大于最小值。且随着功率 系数值相对较小，因此，这里只考虑到 4 次谐波的
的增加，线性模型和非线性模型的最大声压增长百 影响。
分比也随之增大。当输入功率低于 5 W 时，线性模
表 4 不同声功率时 f n 的振幅 (A) 与 f 1 的振幅之比
型和非线性模型的声场分布差异不显著(p > 0.05)；
Table 4 The ratio of the acoustic pressure
当输入功率超过 5 W 时，声波传播的非线性效应不
amplitude (A) in f n to the amplitude in f 1
可忽视(p < 0.05)。
at different acoustic powers
图6为输入声功率为0.4 W和10 W 时，在线性
和非线性模型中分别绘制的焦点处的声压幅值频 声功率/W Af 2 /Af 1 Af 3 /Af 1 Af 4 /Af 1
谱。表4为非线性模型中，声功率为0.4 W、1.5 W、5 0.4 0.0752 0 0
W、10 W、15 W 的 n 次谐波 f n 振幅与基波 f 0 振幅 1.5 0.1247 0 0
的比值。 5 0.2477 0.0781 0.0275
10 0.3438 0.1483 0.0733
由图 6 可知，随着功率的增加，非线性模型中
15 0.4066 0.2075 0.1212
会出现高次谐波，而线性模型中只有基频。由表 4