Page 189 - 《应用声学》2024年第1期

第 43 卷 第 1 期 徐慧等： 高频聚焦超声声场和温度场的仿真研究 185

100 低于 5 W 时，线性模型和非线性模型的温度场分布
差异不显著(p > 0.05)；当输入功率超过 5 W 时，需
80 要考虑高次谐波对温度造成的影响。
ພए/C 3.3 激励声功率对声场和温度场的影响

60 为了研究非线性模型中激励声功率对声场和
ພӤ
温度场分布的影响，在换能器曲率半径为 12 mm、
40 开口直径为 20 mm、加热时间为 10 ms 时，对 5 W、
6 8 10 12 14 16
10 W 和15 W三种输入声功率进行了仿真。图9(a)
ᣉՔᡰሏ/mm
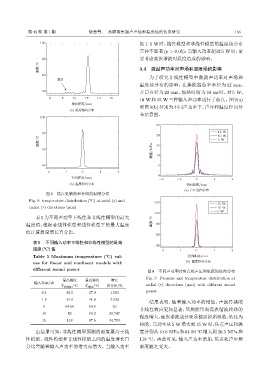
和图 9(b) 分别为不同声功率下，声压和温度径向分
(a) ພएᣉՔѬ࣋
布示意图。
100
25
15 W
80 20 10 W
ພए/C 15 5 W
ࣨϙ/MPa 10
60

40 5
-2 -1 0 1 2
0
य़Քᡰሏ/mm -2 -1 0 1 2
(b) ພएय़ՔѬ࣋ य़Քᡰሏ/mm
(a) ܦԍय़ՔѬ࣋
图 8 焦点处轴向和径向的温度分布
Fig. 8 temperature distribution ( C) at axial (z) and
◦
120
15 W
radial (r) directions (mm) 10 W
5 W
100
表5 为不同声功率下线性和非线性模型的最大
温度值，根据非线性模型和线性模型下的最大温度 ພए/C 80
值计算温度增长百分比。
60
表 5 不同输入功率下线性和非线性模型的最高
40
温度 (℃) 值 -2 -1 0 1 2
Table 5 Maximum temperature ( C) val- य़Քᡰሏ/mm
◦
ues for linear and nonlinear models with (b) ພएय़ՔѬ࣋
different sound power
图 9 不同声功率时焦点处声压和温度的径向分布
Fig. 9 Pressure and temperature distribution at
最高温度 最高温度 增长
输入功率/W
T 非线性 / C T 线性 / C 百分比/% radial (r) directions (mm) with different sound
◦
◦
0.4 38.5 37.9 1.583 power
1.5 44.9 41.6 7.933
结果表明，随着输入功率的增加，声波传播的
5 64.56 53.8 20
非线性效应更加显著，基频能量向高次谐波转移的
10 82 63.2 29.747
程度增大，高次谐波成分更易被组织所吸收，转化为
15 118 87.6 34.703
热能。当功率从5 W增大到15 W时，焦点声压和温
由结果可知，非线性模型预测的温度要高于线 度分别从 10.8 MPa和64.56 C增大到 20.3 MPa和
◦
性模型。线性模型和非线性模型之间的温度增长百 118 C。由此可见，输入声功率增加，焦点处声压和
◦
分比差随着输入声功率的增大而增大。当输入功率 温度随之变大。