Page 114 - 《应用声学》2024年第6期

1290 2024 年 11 月

对频分复用激励信号的影响，将激励压电片和接 500∼621 mm 阶段，几个模态波包的到达时间差较
收压电片位置设置为沿钢板中心线等间距且轴对 小，因此激励信号时长和激励信号的周期数也较
称布置，设置板长变换范围为 500∼2000 mm，变 小，而载波频率主瓣宽度大于压电片扫频曲线的
换步长为 0.1 mm，通过建立模型进行计算得到直 频率范围，最终这个阶段无法生成激励信号；在平
达波 S 0 模态波包和 A 0 模态波包时间差以及子载波 板边长为 621∼773 mm 范围内，激励信号子载波频
个数不同时的子载波频谱主瓣重叠结果图，如图 7 率相近，导致激励信号子频率主瓣重叠为一个，随
所示。 着平板边长尺寸增加，激励信号子载波中心频率
间的差值逐渐增加，重叠的主瓣重叠幅度下降；在
1.2
ᛰѓ-10 dB 平板边长为 774∼863 mm 范围内，频谱上激励信号
ߕᣒฉᮠဋ᧘ԯࣨϙ/V 0.8 预期的子载波中心频率有所差异，且随着平板边长
ᛰѓ-16 dB
有两个频率主瓣，但两个频率主瓣的中心频率与
ᛰѓ-20 dB
尺寸增加，频率主瓣间重叠幅度也不断增加；在平
0.4
板边长为 876∼1232 mm 范围内，激励信号的子载
波主瓣中心频率与所设计的载波频率保持一致，子
0
500 1000 1500 2000
载波主瓣频率间重叠幅度逐渐下降；在平板边长
౜᫂/mm
为1232∼2000 mm，子载波主瓣频率没有重叠部分。
(a) ᣒฉ˔஝˞2௑ߕᣒฉ᧘ԯूए
图 7(b) 是当子载波个数为 3 时，主瓣间重叠的程度
1.6
随平板板长变化的关系图，其变化趋势与图 7(a) 一
ᛰѓ-10 dB 致；在平板边长尺寸增加至 1149 mm 时，信号中三
ߕᣒฉᮠဋ᧘ԯࣨϙ/V 0.8 个主瓣的中心频率与所设计载波频率一致。
ᛰѓ-16 dB
1.2
ᛰѓ-20 dB
频分复用解调
2.2
0.4
利用频分复用激励信号模型计算得到激励信
0 号，并开展实验研究。将激励压电片和接收压电
500 1000 1500 2000
片沿钢板中线轴对称布置，激励压电片距离钢板
౜᫂/mm
(b) ᣒฉ˔஝˞3௑ߕᣒฉ᧘ԯूए 左侧边界 500 mm，接收压电片距离钢板右侧边界
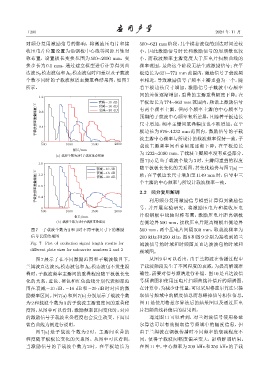
图 7 子载波个数为 2 和 3 时不同平板尺寸下的激励 500 mm，两个压电片间隔 500 mm，取载波频率为
信号长度结果图 200 kHz 和 250 kHz，图 8 和图 9 分别为接收到的兰
Fig. 7 Plot of excitation signal length results for 姆波信号的时域和时频图及直达波波包的时域和
different plate sizes for subcarrier numbers 2 and 3
频域图。
图 7 展示了在不同激励范围和子载波数目下， 从图 9 中可以看出，由于兰姆波在传播过程中
兰姆波直达波 S 0 模态波包和A 0 模态波包不发生混 子载波频段发生了不同程度的衰减，为提高解调准
叠时，子载波频率主瓣间的重叠程度随平板板长变 确性，需要对信号频谱进行补偿。图10 是直达波信
化的关系，蓝色、黑色和红色曲线分别代表频率范 号频谱图和使用压电片扫频曲线补偿后的频谱图。
围在衰减 −10 dB、−16 dB 和 −20 dB 时对应的激 在计算中，为减少计算量，可以采用格兹尔算法只提
励频率区间。图7(a)和图7(b)分别展示了载波个数 取信号频域中的幅度信息而忽略掉信号相位信息，
为 2 和载波个数为 3 的子载波主瓣宽度间的重叠程 图 11 是使用格兹尔算法后的结果图以及通过压电
度图，从图中可以看到，激励频率区间变化时，对应 片扫频曲线补偿后的结果图。
的激励信号子载波重叠程度也会发生改变，下面以 通过图 11 可以看到，对兰姆波信号使用格兹
蓝色曲线为例进行说明。 尔算法可以有效提取信号频域中的幅度信息，但
图 7(a) 是子载波个数为 2 时，主瓣间重叠的 由于兰姆波在钢板传播时不同频率的衰减程度不
程度随平板板长变化的关系图。从图中可以看到， 同，使得子载波间幅度偏差变大，影响解调结果。
当激励信号的子载波个数为 2 时，在平板边长为 在图 11 中，中心频率为 200 kHz 和 250 kHz 的子载