Page 116 - 《应用声学》2024年第6期

1292 2024 年 11 月

4 4
ηՂᮠ៨ 3
ࣨए (arb. units) 2 ࣨए (arb. units) 2 1
ੳᮠజጳ
3

0 1 0
70 120 170 220 270 320 70 120 170 220 270 320
ᮠဋ/kHz ᮠဋ/kHz
(a) РݻฉηՂᝠካፇ౧ (b) ፃ᣿ᛪϪՑᄊРݻฉηՂᝠካፇ౧
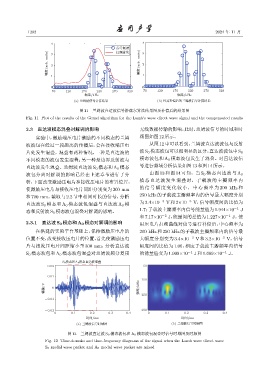
图 11 兰姆波直达波信号格兹尔算法结果图及补偿后的结果图
Fig. 11 Plot of the results of the Gerzel algorithm for the Lamb’s wave direct wave signal and the compensated results

2.3 直达波模态混叠对解调的影响 无线数据传输的影响，此时，兰姆波信号的时域和时

实验中，激励端压电片激励的不同模态的兰姆 频图如图12所示。
波波包在经过一段距离的传播后，会在接收端压电 从图12中可以看到，兰姆波直达波波包与反射
片处发生混叠。混叠有两种情况，一种是直达波的 波S 0 模态波包可以很明显的区分，直达波波包中S 0
不同模态的波包发生混叠；另一种是边界反射波与 模态波包和 A 0 模态波包发生了混叠。对直达波信
直达波发生混叠。兰姆波直达波 S 0 模态和 A 0 模态 号进行频域分析结果如图13和图14所示。
波包分离对解调的影响已经在上述章节进行了分 由图 13 和图 14 可知，当 S 0 模态直达波与 A 0
析，下面改变激励压电片和接收压电片的布置位置， 模态直达波发生混叠时，子载波的主瓣频率内
的信号幅度变化较小， 中心频率为 200 kHz 和
使激励压电片与接收压电片间距分别变为 300 mm
和 700 mm，截取与 2.2 节中相同时长的信号，分析 250 kHz 的子载波主瓣频率内的信号最大幅度分别
直达波 S 0 模态和 A 0 模态波包混叠与直达波 A 0 模 为 3.4×10 −3 V 和 2×10 −3 V，信号幅度间的比值为
态和反射波S 0 模态波包混叠对解调的影响。 1.7；子载波主瓣频率内信号能量值为1.944×10 −1 J
和7.17×10 −2 J，能量间的差值为1.227×10 −1 J。使
2.3.1 直达波S 0 模态和A 0 模态对解调的影响 用压电片扫频曲线对信号进行补偿后，中心频率为
在搭建的实验平台基础上，保持激励压电片的 200 kHz 和 250 kHz 的子载波主瓣频率内的信号最
位置不变，改变接收压电片的位置，首先使激励压电 大幅度分别变为 3.4×10 −3 V 和 3.2×10 −3 V，信号
片与接收压电片间距缩小至 300 mm，分析直达波 幅度间的比值为 1.06，相应子载波主瓣频率内信号

S 0 模态波包和 A 0 模态波包混叠对兰姆波频分复用 的能量值变为1.909×10 −1 J和1.689×10 −1 J。
S 0 വগ֗A 0 വগᄰ᣺ฉຉԯ
0.02 50

0.01
150
ࣨϙ/V 0 ᮠဋ/kHz

-0.01 250

-0.02 350
0 0.1 0.2 0.3 0.4 0 0.1 0.2 0.3 0.4
௑ᫎ/ms ௑ᫎ/ms
(a) РݻฉηՂ௑۫ڏ (b) РݻฉηՂ௑ᮠڏ

图 12 兰姆波直达波 S 0 模态波包和 A 0 模态波包混叠时信号时域图及时频图
Fig. 12 Time-domain and time-frequency diagrams of the signal when the Lamb wave direct wave
S 0 modal wave packet and A 0 modal wave packet are mixed