Page 117 - 《应用声学》2024年第6期

第 43 卷 第 6 期 徐统等： 基于兰姆波的平板频分复用数据传输系统研究 1293

4 ηՂᮠ៨ 5 4
ੳᮠజጳ
ࣨए (arb. units) 3 2 ࣨए (arb. units) 3 2

0 1 1 0
70 120 170 220 270 320 70 120 170 220 270 320
ᮠဋ/kHz ᮠဋ/kHz
(a) ԍႃྟੳᮠజጳˁຉԯηՂᮠ៨ڏ (b) ፃ᣿ᛪϪՑᄊຉԯηՂᮠ៨ڏ

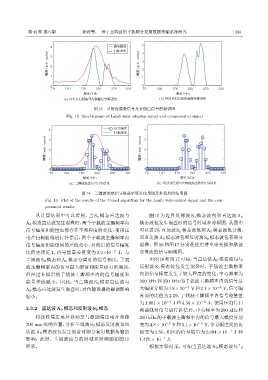
图 13 兰姆波混叠信号及补偿后信号的频谱图
Fig. 13 Spectrogram of Lamb wave aliasing signal and compensated signal

ηՂᮠ៨
4 4
ੳᮠజጳ 3
ࣨए (arb. units) 2 ࣨए (arb. units) 2
3

0 1 1 0
70 120 170 220 270 320 70 120 170 220 270 320
ᮠဋ/kHz ᮠဋ/kHz
(a) РݻฉຉԯηՂᝠካፇ౧ (b) ፃ᣿ᛪϪՑᄊРݻฉຉԯηՂᝠካፇ౧

图 14 兰姆波混叠信号格兹尔算法结果图及补偿后的结果图
Fig. 14 Plot of the results of the Gerzel algorithm for the Lamb wave-mixed signal and the com-
pensated results
从计算结果中可以看到，当 S 0 模态直达波与 图 15 为边界反射波 S 0 模态波包和直达波 A 0
A 0 模态直达波发生混叠时，两个子载波主瓣频率内 模态波包发生混叠时的信号时域和时频图，从图中
信号幅度和能量也都存在不同程度的变化，使用压 可以看到，直达波 S 0 模态波包和 A 0 模态波包分离，
电片扫频曲线进行补偿后，两个子载波主瓣频率内 而直达波 A 0 模态波包和反射波 S 0 模态波包有部分
信号幅度和能量间的差值变小，补偿后的信号幅度 混叠。图 16 和图 17 分别是使用傅里叶变换和格兹
比值更接近 1，信号能量差值变为 2.2×10 −2 J。与 尔算法的信号频域图。
兰姆波 S 0 模态和 A 0 模态分离时的信号相比，子载 由图 16 和图 17 可知，当直达波 A 0 模态波包与
波主瓣频率内的信号最大幅值和能量值有所增加， 反射波 S 0 模态波包发生混叠时，子载波主瓣频率
但经过补偿后的子载波主瓣频率内的信号幅度和 内的信号幅度发生了较大程度的变化，中心频率为
能量差值减小。因此，当兰姆波 S 0 模态直达波与 200 kHz 和 250 kHz 的子载波主瓣频率内的信号最
A 0 模态直达波发生混叠时，对传输数据的解调影响 大幅度分别为4.8 × 10 −3 V和2.1 × 10 −3 V，信号幅

较小。 度间的比值为 2.29，子载波主瓣频率内信号能量值
为 1.881 × 10 −1 J 和 4.34 × 10 −2 J。使用压电片扫
2.3.2 直达波A 0 模态和反射波S 0 模态 频曲线对信号进行补偿后，中心频率为 200 kHz 和
将接收端压电片移动至与激励端压电片相距 250 kHz 的子载波主瓣频率内的信号最大幅度分别
700 mm 处的位置，分析兰姆波 S 0 模态反射波与直 变为4.8 × 10 −3 V和3.1 × 10 −3 V，信号幅度间的比
达波 A 0 模态波包发生混叠对频分复用数据传输的 值变为 1.55，相应的信号能量为 2.604 × 10 −1 J 和
影响，此时，兰姆波信号的时域和时频图如图 15 1.476 × 10 −1 J。
所示。 根据实验结果，可知当直达波 A 0 模态波包与