Page 144 - 《应用声学》2024年第6期

1320 2024 年 11 月

3.2 目标函数及反演流程
3 裂缝宽度反演方法
如果实测波形具有足够的低频带宽，则可以
3.1 反射系数的理论模拟 根据实测波形数据的反射系数和理论反射系数反
假定除了斯通利波外，声波测井频率低于其他 演裂缝宽度。理想情况下，频率的下限越低越好，
模式波的截止频率，即充液井孔中只存在斯通利波， 实际测井时，受限于声波仪器的性能，频率下限在
因此可以认为在测井仪和井壁之间的流体环空中 300∼500 Hz 之间，上限通常为 2∼4 kHz。在反演裂
流体压力是近似均匀的。斯通利波能量集中在井内， 缝参数时，频率的上下限通常作为算法的输入参数，
可以根据数据质量进行动态调整。
井内流体进行轴向活塞式运动，因此可以用一维传
播理论来描述斯通利波在井中的传播特征 [11] 。 采用数值方法进行反演，目标函数是公式 (5)
给出的实际数据反射系数和公式 (6) 给出的理论反
由一维等效波数法可求解出过井裂缝的理论
反射系数： 射系数之间的L2范数：
ω max
2
2
2i(k − k ) sin(k 2 L) ∑ (R D (ω) − Ref(ω, L)) W R (ω), (8)
2
1
2
Ref(ω) = , (6) L2(L) =
(k 1 + k 2 ) e − (k 1 − k 2 ) e ω=ω min
2 −ik 2 L
2 ik 2 L
式(6)中，L 为裂缝宽度，k 1 和k 2 分别为裂缝处和上 式 (8) 中，W R 是一个与频率相关的加权函数，其频
下地层处的斯通利波波数。在刚性地层中，上下地 率边界根据数据质量进行动态调整，频率界限之内
层的波数为k 1 = ω/v f ，裂缝处的波数为 权重设为 1，频率界限外的权重设为 0。图 9 为某深
v 度点实际反射系数与最佳拟合理论反射系数结果，
u (1)
ω u 2 H 1 (k 0 R)
k 2 = t 1 − , (7) 红点为实际数据的反射系数，蓝色实线为理论反射
v f k 0 R H (1) (k 0 R)
0 系数。由于波场分离中的噪声和混叠，高频范围的
式(7)中，R 为井眼半径，v f 为流体声速，H (1) 和H (1) 反射系数通常是不准确的，因此需要设置加权函数
0 1
分别为 0 阶和 1 阶汉克尔函数。对于刚性裂缝面， 来去除高频部分，如图 9 中绿色框线显示加权范围
k 0 = ω/v f ，即自由流体空间波数。 为 0.5∼3.5 kHz，加权范围外权重设为 0。图 10 第 2
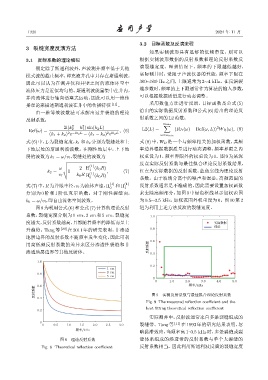
图8为利用公式(6)和公式(7)计算的理论反射 道为利用上述方法反演的裂缝宽度。
系数，裂缝宽度分别为 1 cm、2 cm 和 5 cm，裂缝宽 1.0
度越大，反射系数越高，且都随着频率的降低而呈上 ࠄᬅ஝૶
ေ᝷
升趋势。Tang 等 [20] 在 2011 年的研究表明，非渗透 0.8
地层边界的反射系数不随频率发生变化，因此可利
0.6
用高低频反射系数的差异来区分渗透性裂缝和非 Ԧ࠱ጇ஝
渗透地层边界等其他反射体。 0.4

1.0
0.2
1 cm
2 cm
0.8
5 cm
0
0 1.0 2.0 3.0 4.0 5.0
0.6 ᮠဋ/kHz
Ԧ࠱ጇ஝ 图 9 实测反射系数与最佳拟合理论反射系数
0.4
Fig. 9 The measured reflection coefficient and the
best fitting theoretical reflection coefficient
0.2
实际测井中，反射波通常来自多条裂缝组成的
0 [11]
0 0.5 1.0 1.5 2.0 2.5 3.0 裂缝带。Tang 等 在 1993 年的研究结果表明，忽
ᮠဋ/kHz
略黏滞效应，当频率高于 0.5 kHz 时，多条裂缝或裂
图 8 理论反射系数 缝体系组成的渗透带的反射系数与单个大裂缝的
Fig. 8 Theoretical reflection coefficient 反射系数相当。因此利用斯通利波反演的裂缝宽度