Page 142 - 《应用声学》2024年第6期
P. 142
1318 2024 年 11 月
达波到时处的反射波幅度很小,因此用幅度平方 X060∼X064 m 处的反射源,而此反射波同时也处
法计算的反射源位置图上没有明显的反射源,而 于用于计算 X064 m 处反射系数的深度段内,影响
能量堆叠法虽然在分辨率上没有幅度平方法高,但 了X064 m处反射系数的计算。因此,在进行反射系
是在 X060 m 处有一个明显的峰值,不会因为反射 数计算之前,需先消除干扰波形。第一种消除干扰
波幅度的影响而识别不出反射源。图 5 最右侧给 波形的方法为:在目标反射源深度和上方邻近反射
出了 X058∼X061 m 和 X063∼X067 m 处的电成像 源深度之间选择一波形作为模板波形,假设反射堆
结果,可以看到 X060 m、X063.5 m、X066.2 m 和 叠深度处的干扰波形为模板波形的时移和幅度缩
X066.8 m处存在明显的高导缝,与反射源识别结果 放,通过深度-深度互相关法可以确定模板波形到目
一致,验证了斯通利波定位反射源的有效性。 标波形的时移和幅度缩放比例。从目标波形中减去
时移和缩放后的模板波形,即可消除干扰波形。另
2.2 现场数据的斯通利波反射系数计算
一种消除干扰波形的方法是开窗法。以反射波峰值
2.2.1 传统计算方法
为中心开一锥形窗口 (例如 Tukey 窗),并将此窗口
将波场分离后的波形进行傅里叶变换,得到直
与反射堆叠深度内的各波形相乘,即可消除干扰波
达波频谱 D(ω) 和下行反射波频谱 R(ω),则斯通利
形。各深度锥形窗口位置由直达波到时和定位反射
波反射系数频谱计算公式如下 [10] :
源时所用的斯通利波慢度共同决定。
R(ω)
r(ω) = , (3)
D(ω) X055
为了避免 D(ω) 趋近于 0 时 r(ω) 产生假峰,可将公
式(3)修正如下 [10,19] :
X060
R(ω)D (ω)
∗
r(ω) = , (4)
max[D(ω)D (ω), cK]
∗
式 (4) 中, D (ω) 为 D(ω) 的 共 轭 频 谱, K 为 ງए/m X064
∗
D(ω)D (ω)的峰值,系数c一般取.01。 X065
∗
2.2.2 反射堆叠法
反射系数的传统计算方法是将每个深度点的 X070
反射波频谱直接与直达波频谱相除,忽略了来自其
他深度的反射波对该深度的干扰,因此利用此方法
计算的反射系数峰值与实际反射源的位置有偏差。 X075 0 2000 4000 6000 8000
下面介绍一种新方法,根据 2.1 节定位的反射源位 ᫎ/ms
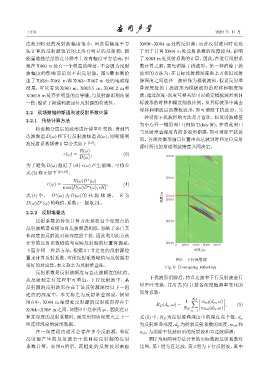
置来计算反射系数,可使反射系数峰值与反射源有 图 6 下行反射波
很好的对应性,本文称之为反射堆叠法。 Fig. 6 Downgoing reflection
反射系数是反射波幅度与直达波幅度的比值。
干扰波形消除后,将直达波和下行反射波进行
从反射源定位过程中可看出,下行反射波中,某
傅里叶变换,并用式 (5) 计算各深度随频率变化的
反射源的反射波形存在于该反射源深度以下一组
反射系数:
连续的深度中,本文称之为反射堆叠深度,例如
N S
图 6 中,X064 m 深度处反射源的反射波形存在于 1 ∑ w ref (d n , ω)
R D (d p , ω) = , (5)
X064∼X068 m 之间,如图 6 中红框所示。因此在计 N S n=1 w dir (d n , ω)
算某深度的反射系数时,需要用到该深度点之下一 式 (5) 中,N S 为反射堆叠深度中的深度点个数,d n
组连续深度的波形数据。 为反射堆叠深度,d p 为所求反射系数的深度,w ref 和
在一深度段内通常会存在多个反射源,邻近 w dir 为消除干扰波形后的反射波和直达波频谱。
反射源产生的反射波会干扰目标反射源的反射 图7为用两种方法计算的实际数据反射系数对
系数计算。如图 6 所示,蓝框处的反射波形来自 比图,第 1 道为直达波,第 2 道为下行反射波,其中