Page 148 - 《应用声学》2025年第1期

144 2025 年 1 月

体实验设备如图 7 所示。高速采集卡将采集到激发 取 8 只换能器各自 20 s 内的超声回波信号，将其中
波与超声信号，进而轮流采集 8 只换能器的回波信 两组波形数据预处理后，应用DTW 算法处理，结果
号，为保证实验数据的可靠性，每只换能器的采样 如图9所示。根据DTW算法寻找两个时间序列 (波
时间为 20 s，则采集单只换能器的回波信号数目达 形信号) 各局部距离累加和最小的规整路径，完成
上千个。 两个可非等长序列之间的最短距离的计算。计算得

将采集卡采集的原始数据保存，利用 Python 出 DTW(Q, C) 具体数值，用来评价两个波形的相
工具对原始数据处理为时序信号如图 8 所示，并提 似性。

฾ត૱ᑟ٨
ᡔܦฉԦ࠱ྟ
ᰴᮠ஝૶᧔ᬷӵ
ηՂ฾តኮ᥋ ॠ฾ԍႃ૱ᑟ٨

ࠄᰎ
नԧ౜
ᩛ
ႃ
෉

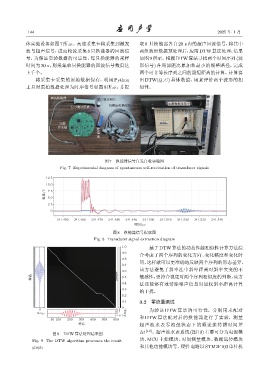
图 7 换能器信号自发自收实验图
Fig. 7 Experimental diagram of spontaneous self-receivation of transducer signals

12.5
10.0
ႃԍ/V 7.5
5.0
2.5
0
341.450 341.460 341.470 341.480 341.490 341.500 341.510 341.520 341.530 341.540
௑ᫎ/ms
图 8 换能器信号提取图
Fig. 8 Transducer signal extraction diagram
1.0
基于 DTW算法的动态性能相似性计算方法综
0.9
合考虑了两个序列的变化方向、变化幅度和变化时
0.8
间，这样就可以更准确地反映两个序列的形态差异，
0.7
该方法避免了斜率法中斜率距离对斜率突变的不
0.6
ನֶ %JTUBODF 0.5 敏感性，更符合视觉对两个序列相似度的判断，该方
0.4 法还能够有效消除噪声信息对加权斜率距离计算
0.3
的干扰。
0.2
0.1 3.2 零流量测试
0
0 0.2 为验证 DTW 算法的可行性，分别用未配对
0.1
Amp. -0.1 Amp.
0
50 100 200 300 400 500 600 和 DTW 算法配对后的换能器进行了实验，测量
ನֶ 超声波水表零流量状态下的顺逆流传播时间差
图 9 DTW 算法处理结果图 ∆t [10] 。超声波水表系统 (图 10) 主要可分为电源模
Fig. 9 The DTW algorithm processes the result 块、MCU 主控模块、时间测量模块、数据远传模块
graph 和其他功能模块等。硬件电路以STM2F103单片机