Page 205 - 《应用声学》2025年第1期

第 44 卷 第 1 期 黄应来等： 车内轰鸣声反相位抵消方法研究及应用 201

其中，P i 和 P r 分别为入射声波和反射声波的声压 从图 6 所示耦合方程解的构成可知，只有当前
幅值。令 r i 为入射声压与反射声压的比值，表示为 风挡的固有频率低于尾门固有频率时，才能使其低
式 (6)： 于耦合频率，从而实现相位−180 调整。此时，前风
◦
P i Z s0 + ρc 1 − Y v0 ρc jσπ 挡和尾门固有频率都低于耦合频率，相位都发生过
r i = = = = |r i | e , (6)
◦
P r Z s0 − ρc 1 + Y v0 ρc −180 变化，也即前风挡与尾门同相位时，车内前排
其中，Y v0 是前风挡的振动导纳，表示为式(7)： 的声压级最小。因此，拟将前风挡固有频率从48 Hz
调整到38 Hz，对应耦合频率从41 Hz提高到48 Hz，
jωS
Y v0 = , (7) 驻波振型如图 8 所示，可以看出前排声压幅值大幅
2
−ω M 0 + K 0
降低。
其中，|r i |为幅值，σπ为相位差。
将式 (6) 带入式 (5) 得到总声压幅值随位移 x TP r
3
的变化规律如式(8)所示： 2
√ 1 Ғଆ݀ౣͯᎶ
( λ ) ܦԍ/Pa 0
2
P = P r 1 + |r i | + 2|r i | cos 2k x − σ . (8) -1
4 -2
-3
对于特定的频率解，此即驻波振型。进一步推 0 0.5 1.0 1.5 2.0 2.5 3.0 3.5
导可知，当位移 x、波长 λ 和相位系数 σ 满足式 (9) ͯᎶ/m
(a) Ғ᮳૕48 Hz௑ᄊ᯿ฉ૝ی
时，声压为极小值。 TP r
3
λ 2
( )
2k x − σ = ±(2n + 1)π, 1
4 ܦԍ/Pa 0
n = 0, 1, 2, · · · , (9) -1
-2
-3
因此，当前风挡的振动导纳取某一相位时，可实现特 0 0.5 1.0 1.5 2.0 2.5 3.0 3.5
定频率的驻波在指定位移处声压幅值为极小值。 ͯᎶ/m
(b) Ғ᮳૕38 Hz௑ᄊ᯿ฉ૝ی
分析前风挡不同振动相位对车内前排位置
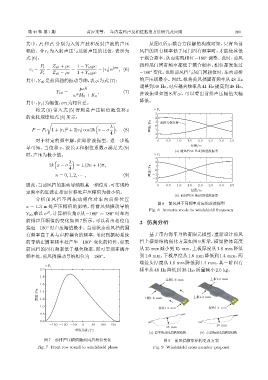
图 8 前风挡不同频率对应的驻波振型
x = 1.3 m 处声压幅值的影响，将前风挡振动导纳
Fig. 8 Acoustic mode to windshield frequency
Y v0 乘以 e ，计算相位角 θ 从−180 ∼ 180 时车内
jθ
◦
◦
前排声压幅值的变化如图 7 所示，可以看出相位角 3 仿真分析
接近−180 时声压幅值最小。当前状态前风挡的固
◦
有频率高于其与声腔耦合的频率，考虑到振动系统 基于带内饰车身的有限元模型，重新设计前风
的导纳在固有频率处产生 −180 变化的特性，如果 挡上横梁结构弱化方案如图 9 所示，横梁腔体高度
◦
前风挡的固有频率低于耦合频率，即可实现在耦合 从 35 mm 减小到 15 mm，上板厚度从 1.6 mm 降低
频率处，前风挡振动导纳相位为−180 。 到 1.0 mm，下板厚度从 1.6 mm 降低到 1.4 mm，两
◦
端接头厚度从 1.6 mm 降低到 1.4 mm，其一阶固有
TP r
2.0 频率从48 Hz降低到38 Hz，质量减小2.5 kg。
1.8
ʽ౜1.6 mm ʽ౜1.0 mm
1.6
ܦԍ/Pa 1.4 ʽ౜1.6 mm ʽ౜1.2 mm
1.2
1.0
ଌ݀1.6 mm ଌ݀1.4 mm
0.8
0.6
-150 -100 -50 0 50 100 150 20 mm
35 mm
ᄱͯᝈए/(O)
(a) ԔᢼᄊҒ᮳૕ഷ್ፇ౞ (b) வವᄊҒ᮳૕ഷ್ፇ౞
图 7 前排声压幅值随前风挡相位变化 图 9 前风挡横梁结构更改方案
Fig. 7 Front row sound to windshield phase Fig. 9 Windshield cross member proposal