Page 119 - 《应用声学》2025年第3期

第 44 卷 第 3 期 梁启慧等： 不完全深海声道下多途到达结构特性及测距 653

∫
z r √ 加计算声场，而模态和距离无关，只和频率有关，因
2
2
ξ 02 = n (z) − cos (α 02 )dz
此在30 km以后依然存在02 − 22时延曲线，与实验
z s
∫
z r √
2
2
+ 2 n (z) − cos (α 02 )dz 数据相吻合(图10(b))。
z rev
ॆʷӑࣨϙ
+ R cos(α 02 ). (19) 2.5 0.55
同理声线01程函为
2.0 0.50
∫
z r√
2
2
ξ 01 = n (z)−cos (α 01 )dz+R cos(α 01 ), (20)
z s 1.5 0.45
其中，α 01 为只经过一次海底反射声线的声源掠 ௑णࣀ/s
射角。 1.0 0.40
0
02ܦጳ
α shw 0.5 0.35
200 ॖӝܦጳ
α  ଌஆӭЋ
400
0 0.30
0 10 20 30 40
600 ᡰሏ/km
ງए/m 800 (a) BELLHOPᝠካᡰሏ-௑णڏ
1000 ॆʷӑࣨϙ
2.5 0.65
1200
1400 0.60
2.0
1600
0.55
0 5 10 15 20 25 30 35 40
ᡰሏ/km 1.5
图 9 声影区声线图 ௑णࣀ/s 0.50
1.0
Fig. 9 Sound map of the sound shadow area 0.45
在7 ∼ 27 km范围内计算时延差： 0.5
0.40
∆t 11−01 = (ξ 11 − ξ 01 )/c 0 . (21)
0 0.35
0 10 20 30 40
在27∼51 km范围内计算时延差： ᡰሏ/km
(b) KRAKENᝠካᡰሏ-௑णڏ
∆t 22−02 = (ξ 22 − ξ 02 )/c 0 . (22)
2200
综合利用式(7)∼(8)、式(21)∼(22)，得到了实验 f=100 Hz, z s =200 m, z r =1640 m
2000
环境下的多途时延差与收发距的关系(图10)。图 10 1800 र(7)~(8)ᝠካ
र(21)~(22)ᝠካ
中红色部分分别表示一次海底一次海面反射声线 1600 BELLHOPᝠካ
与只经过一次海底反射后反转声线的多途时延差 1400
(11 − 01)、两次海底两次海面反射声线与只经过两 ௑णࣀ/ms 1200
次海底反射后反转声线的多途时延差(22 − 02)。采 1000 Ğ 11Ē22
800
用相同的环境参数，分别使用 KRAKEN 和 BELL- 600 00Ē11 ğ
HOP 进行宽带声场计算，并对求得的声压进行反 400
ğ01Ē11 ğ02Ē22
傅里叶变换，可以得到距离 -时延 (r-t) 二维图案。 200 0 5 10 15 20 25 30 35 40 45 50
与式 (7)∼(8)、式 (21)∼(22) 计算得到的时延差曲线 ᡰሏ/km
(c) ܦູງए200 m, ௑णࣀˁᡰሏТጇ
进行拟合，可以发现均比较好的吻合。值得注意
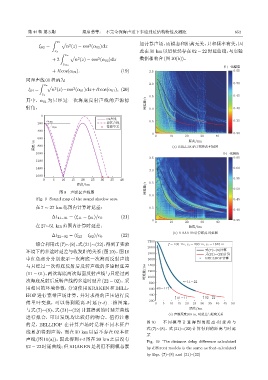
的是，BELLHOP 在计算声场时是将不同本征声 图 10 不 同 模 型 计 算 得 到 的 距 离 -时 延 差 与
式 (7)∼(8)、式 (21)∼(22) 计算得到的距离与时延
线累加得到声场，而在 30 km 以后不存在 02 本征
差
声线 (图 10(a))，因此得到 r-t 图在 30 km 之后没有
Fig. 10 The distance delay difference calculated
02 − 22 时延曲线；但KRAKEN 是利用不同模态累 by different models is the same as that calculated

by Eqs. (7)–(8) and (21)–(22)