Page 116 - 《应用声学》2025年第3期

650 2025 年 5 月

其中，z s 为声源深度，z r 为接收器深度，n(z) 为深度 00声线程函为
∫
z r √
z 处的折射率，R 为接收距离，α 为声源处掠射角，c 0 2 2
ξ 00 (r, z) = n (z) − cos (α 00 )dz
为声源处声速。 z s
因此，两次海底反射两次海面反射 (为书写方 + R cos α 00 , (6)
便写为“22”，即声线接触海面 2 次，接触海底 2 次， 其中，α 00 、α 11 、α 22 分别为声线方向角的初始角，称
下同)、一次海底反射一次海面反射 (写为“11”) 和 为声源处掠射角。
直达声的程函(写为“00”)分别可以写为 故时延差可以表示为
22声线程函为
∆t 22−11 = (ξ 22 − ξ 11 )/c 0 , (7)
∫
z r √
2
2
ξ 22 (r, z) = n (z) − cos (α 22 )dz ∆t 11−00 = (ξ 11 − ξ 00 )/c 0 . (8)
z s
∫
z r √ 利用 BELLHOP 进行仿真，声源频率设置为
2
2
+ 4 n (z) − cos (α 22 )dz
0 100 Hz，声源深度 200 m，接收深度 1640 m，声速
+ R cos(α 22 ), (4) 剖面如图 1(b) 所示，获得了不同收发距离时的声线
到达结构与声线到达时间 (图 5)，进而利用所推导
11声线程函为
的多途时延差计算公式以及 BELLHOP 方法计算
∫
z r √ 了不完全深海声道情况下多途时延差与距离的关
2
2
ξ 11 (r, z) = n (z) − cos (α 11 )dz
系 (图 6)。结果表明，多途时延差随距离增加而减
z s
∫
z r √ 小，但是在 10 km 和 25 km 以远存在反转声线。为
2
2
+ 2 n (z) − cos (α 11 )dz
0 此，本文利用Snell定律，在3.2节对不完全深海声道
+ R cos(α 11 ), (5) OBS接收到的声线结构进行了进一步研究。
0 2.0
00ܦጳ
200 1.8 01ܦጳ
1.6 11ܦጳ
400 1.4 22ܦጳ
600 1.2
ງए/m 800 ࣨए/10 -4 1.0
1000 0.8
1200 0.6
0.4
1400
0.2
1600 0
0 1 2 3 4 5 3 4 5 6 7 8 9 10 11
ᡰሏ/km ҂᣺௑ᫎ/s
(a) ଌஆᡰሏ5 kmܦጳڏ (b) ଌஆᡰሏ5 kmܦጳ҂᣺௑ᫎ
0 4.5
11ܦጳ
200 4.0 22ܦጳ
400 3.5 Х̵ܦጳ
3.0
600
ງए/m 800 ࣨए/10 -5 2.5
2.0
1000
1.5
1200
1.0
1400
0.5
1600
0
0 2 4 6 8 10 12 14 16 18 20 14 15 16 17 18
ᡰሏ/km ҂᣺௑ᫎ/s
(c) ଌஆᡰሏ20 kmܦጳڏ (d) ଌஆᡰሏ20 kmܦጳ҂᣺௑ᫎ
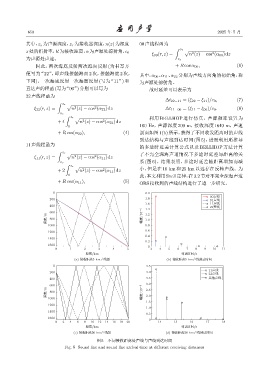
图 5 不同接收距离处声线与声线到达时间
Fig. 5 Sound line and sound line arrival time at different receiving distances