Page 162 - 《应用声学》2025年第3期

696 2025 年 5 月

相互传递关系为 总的传递矩阵[T ]，
           

v 1 v 1 v 1 v 1 v 1 v 1
           
        n    
 v 3   v 3   v 3   v 3  ∏  v 3   v 3 
= [M d ][M 0 ] = [T T i ] ,
  −1       = [T T i ]   = [T ]   .
           
σ 33  σ 33  σ 33  σ 33  i=1 σ 33   σ 33 
           

σ 13 σ 13 σ 13 σ 13 σ 13 σ 13
d 0 0 D 0 0
(6) (7)
其中，[T T i ]即为第i层介质的应力应变传递矩阵。 1.2 求解反射、透射系数
在不同固体介质分界面上，应力应变是连续一 应用正交各向异性层合板上下表面的法向应
致，完全传递，所以根据矩阵的连乘关系，可以得到 力、法向位移连续性条件 [20] ，其反射系数R 和透射
多层介质的透射端界面到入射端界面的应力、振速 系数D 分别为

2
2
n+1
2
1
jk 13 (jm 32 k 13 + m 33 ρ 1 ω ) − (jm 22 k 13 + m 23 ρ 1 ω )ω ρ n+1
R = n+1 , (8)
2
jk (jm 32 k 13 + m 33 ρ 1 ω ) + (jm 22 k 1 2 2
13 13 + m 23 ρ 1 ω )ω ρ n+1
ρ 1 jk n+1 (1 − R) ൤̔ՊՔप Պࡏె
13
D = 1 , (9) ൤̔ ভѸएᅾ᫼ ܭՌ
ρ n+1 jk m 22 + m 23 ρ 1 ω 2 நԠ஝
13 ՊՔ ెந
पভ ՊՔपভె ݃ᔇ
其中，m ik = T ik − T i1 T 4k /T 41 ，ρ 1 、ρ n+1 表示入射端 ౜͜ நฉүவሮ ࡏፇ
᤬ᅾ ౞
1
和透射端的流体介质密度，k 、k n+1 表示入射端和 ᫼ข Պࡏऄҧnj ᩔࡏ
13 13 ͯረ͜᤬ᅾ᫼ ᝺Ꮆ
透射端的压缩波波数，
ω ܭՌెந݃ᔇࡏፇ౞ܦߦጇ஝
1
k = cos θ i , (10)
13
c 0
ω Ԧ࠱ጇ஝ ᤩ࠱ጇ஝ ծܦጇ஝
n+1
k 13 = cos θ t . (11)
c 0
К࠱ག
ᄬಖї͵വی
2 基于曲面单元的目标强度数值计算方法 ᄬಖᎪಫηৌ జ᭧౜ڱЋ ଌஆག
ᮠဋ
2.1 Kirchhoff高频近似
传递矩阵法与曲面板块元法相结合具体步骤： ᝠካፇ౧
首先设置复合材料夹芯层结构的材料参数以及铺 ᄬಖूए ங࠱ܦڤ
层参数，求解表面的反射系数；其次，将目标整体几
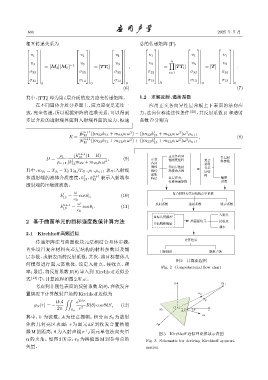
图 2 计算流程图
何模型进行面元离散化，设定入射点、接收点、频
Fig. 2 Computational flow chart
率；最后，将反射系数R(θ)导入到 Kirchhoff近似公
式 [13] 中，计算流程如图2所示。
y M 
考虑到非刚性表面的反射系数 R(θ)，在收发合
置情况下计算散射声场的Kirchhoff近似为 r 
∫∫ 2ikr r
ikA e
φ S (r) = − R(θ) cos θdS, (12)
2π r 2 O
S 0 S  dS θ x
其中，k 为波数；A 为任意振幅；积分面 S 0 为散射 n
体的几何亮区表面；r 为面元 dS 到收发合置换能 z
器 M 的距离；θ 为入射声线 r 与面元单位法向矢量
图 3 Kirchhoff 近似理论推导示意图
n 的夹角。如图 3 所示，r 0 为换能器 M 到参考点的 Fig. 3 Schematic for deriving Kirchhoff approxi-
矢量。 mation