Page 164 - 《应用声学》2025年第3期

698 2025 年 5 月

从图 6 中可以看出，在 100 Hz∼10 kHz 频率范 从图 8 中可以看出，在 500 Hz∼10 kHz 频段范
围内，复合材料夹芯层结构的传递矩阵法结果与有 围内，复合材料夹芯层结构球壳的有限元仿真结果
限元仿真结果比较吻合，说明通过传递矩阵法求复 与板块元结果比较相近，主要特征也基本吻合。考
合材料夹芯层结构的反射、透射系数是可靠的，并 虑到有限元计算量大，计算时间长，因此本文采用曲
将此反射系数导入到曲面板块元中，研究复合材料 面板块元法计算水下复杂目标声散射特性，并分析、
夹芯层结构壳体的目标声散射特性。 讨论复合材料夹芯层结构十字舵的目标强度。
1.0
ܱᦊܦڤ

0.8 ݃ࡏܭՌ
ెநုܧ
Ԧ࠱ጇ஝ 0.6

0.4
ᄾቇ

0.2 దᬍЋ
͜᤬ᅾ᫼ข ߹ᎿӜᦡࡏ
0
0 2000 4000 6000 8000 10000
ᮠဋ/Hz 图 7 有限元二维轴对称声散射计算模型
(a) Ԧ࠱ጇ஝ࠫඋፇ౧
Fig. 7 Finite element two-dimensional axisym-
1.0
దᬍЋ metric acoustic scattering calculation model
͜᤬ᅾ᫼ข
0
0.8
-5
ᤩ࠱ጇ஝ 0.6 -10
ᄬಖूए/dB -20
-15

0.4 ౜ڱЋ
-25
దᬍЋ
-30
0.2
0 2000 4000 6000 8000 10000
-35
ᮠဋ/Hz
(b) ᤩ࠱ጇ஝ࠫඋፇ౧ -40
0 2000 4000 6000 8000 10000
ᮠဋ/Hz
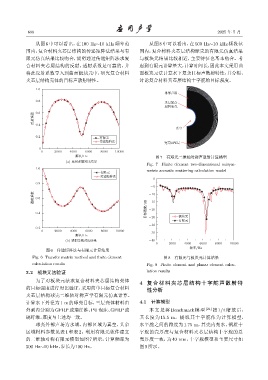
图 6 传递矩阵法与有限元计算结果
Fig. 6 Transfer matrix method and finite element 图 8 有限元与板块元计算结果
calculation results Fig. 8 Finite element and planar element calcu-

3.2 板块元法验证 lation results
为了对板块元法求复合材料夹芯层结构壳体
4 复合材料夹芯层结构十字舵声散射特
的目标强度进行对比验证，采用简单目标复合材料 性分析
夹芯层结构球壳二维轴对称声学有限元仿真计算。
计算水下外径为 1 m 的球壳目标，三层壳体材料由 4.1 计算模型
外到内分别为 GFRP 玻璃纤维、PU 泡沫、GFRP 玻 本文是将 Benchmark 模型 [21] 按 1/4 缩放后，
璃纤维，厚度与上述均一致。 其长度为 15.5 m，提取其十字舵作为计算模型，
球壳外部声场为水域，内部区域为真空，其余 水平舵之间的跨度为 1.75 m，其壳内充水，钢质十
区域材料参数见表 1 和表 2。利用有限元软件建立 字舵的壳厚度与复合材料夹芯层结构十字舵的总
的二维轴对称有限元模型如图 7 所示，计算频率为 壳厚度一致，为 40 mm，十字舵模型和主要尺寸如
500 Hz∼10 kHz，步长为100 Hz。 图9所示。