Page 238 - 201805

820 2018 年 9 月

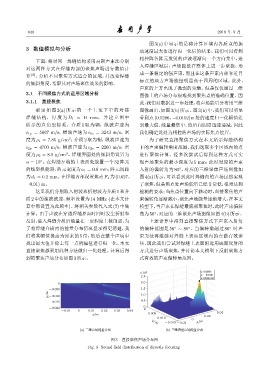
图 3(a) 中显示的是将计算区域内各质点的振
3 数值模拟与分析
动速度最大值进行归一化后的结果。我们可以看到
相控阵各阵元发射的声波逐渐向一个方向集中，进
下面，将对同一焊缝结构采用高斯声束法分别
入焊缝区域后，声场能量在整体上进一步聚拢，形
对这两种方式在焊缝内部的聚焦声场进行数值计
成一条稳定的强声束，而且在这条声束内部靠近目
算 [8] ，分析不同聚焦方式适合的区域，并改变焊缝
标点的地方声场能量明显高于四周的区域。此外，
的倾斜角度，考察其对声场聚焦效果的影响。
声束的上方出现了微弱的旁瓣。但是仅仅通过二维
3.1 不同聚焦方式的适用区域分析 图像上的声场分布很难找到聚焦点的准确位置。因

3.1.1 直接聚焦 此，我们对数据进一步处理，将声场能量分布用三维
确定如图 2(a) 所示的一个上宽下窄的对接 图像画出，如图3(b)所示。图3(b)中，我们可以明显
焊缝结构，厚度为 D 1 = 14 mm，并建立图中 看到点 (0.0286，−0.0102)m 处的速度归一化幅值达
所示的直角坐标系。介质 1 取为钢，纵波声速为 到最大值，能量最集中，然后向四周迅速递减，因此
c 1p = 5867 m/s，横波声速为 c 1s = 3243 m/s，密 我们确定此处为相控阵声场的实际焦点位置。
3
度为 ρ 1 = 7.85 g/cm ；介质 2 取为铜，纵波声速为 为了研究直接聚焦方式在本文所示焊缝结构
c 2p = 4700 m/s，横波声速为 c 2s = 2260 m/s，密 下的声束偏转角度范围，我们选取多个区域内的点
度为 ρ 2 = 8.9 g/cm 。焊缝界面处的倾斜角设置为 进行聚焦计算。经多次尝试后得到这种方式可实
3
α = 10 。在焊缝左端的上表面处放置一个 32 阵元 现声场聚焦的最小深度为 5 mm，此时对应的声束
◦
的线型换能器，阵元宽度为 a 1 = 0.8 mm，阵元间距 入射的偏转角为 80 ，对应的三维聚焦声场图像如
◦
为d 1 = 0.2 mm。在焊缝内部设置焦点F 1 为(0.027， 图 4(a) 所示，可以看到此时焊缝内的声场虽然实现
−0.01) m。 了聚焦，但是焦点处声场能量已经非常低，很难达到
这里我们分别取入射波和折射波为介质 1 和介 检测的要求；当焦点位置向下移动时，直接聚焦的声
质 2 中的横波波速，频率设置为 14 MHz (在本文计 束偏转角逐渐减小，聚焦声场能量逐渐增大，在本文
算中都设置为此频率)。将相关参数代入式 (7) 中做 模型下，当声束在焊缝最底部聚焦时，此时声束偏转
计算。由于声波在穿透焊缝界面时同时发生折射和 角为56 ，对应的三维聚焦声场图像如图4(b)所示。
◦
反射，进入焊缝介质后能量在一定程度上被削弱，为 上述计算中得到直接聚焦方式下声束入射角

了将焊缝介质内的能量分布情况显示得更清楚，我 的偏转范围是 56 ∼ 80 。当偏转角超过 80 时声
◦
◦
◦
们将其幅值提高为原来的 5 倍，然后在整个声场中 束无法再继续对焊缝上表面区域内的点做有效聚
找出最大值并除上每一点的幅值进行归一化，本文 焦，因此我们尝试对焊缝上表面附近用底面反射的
直接聚焦都采用此种方法做归一化处理。计算后得 方式进行声场聚焦，并讨论本文模型下反射聚焦方
到的聚焦声场分布如图3所示。 式有效的声束偏转角范围。

T10 4 x: 0.02856
2.5 y: -0.0102
z: 2.203e+04
 2.0
֓⊲ 1.5
y/m ֓⊲ 1.0
֓⊲ 0.5
0
֓⊲ 0
֓⊲  ⊲ ⊲ ⊲ ⊲ 0.04
x/m -0.005 0.02
-0.010
0
-0.015 -0.02 x/m
y/m
(a) ̄፥ܦڤᑟ᧚Ѭ࣋ (b) ʼ፥ᅌᓤܦڤᑟ᧚Ѭ࣋
图 3 直接聚焦声场分布图
Fig. 3 Sound field distribution of directly focusing