Page 239 - 201805

第 37 卷 第 5 期 史慧宇等： 焊缝结构中超声相控阵聚焦声场的数值模拟及分析 821

T10 4
2.5 T10 4
2.5 x: 0.03
y: -0.0168
2.0 2.0 z: 1.963e+04
1.5
1.5
1.0
x: 0.02396
1.0 0.5
y: -0.00462
z: 4356
0
0.5 0
0.04
-0.01 0.02
0  0
֓⊲  ⊲ ֓⊲ y/m -0.02 -0.02 x/m
x/m ⊲ y/m
(a) 5 mmງएܫᄊᐑཥܦڤ (b) ཝᎋతअᦊᄊᐑཥܦڤ
图 4 直接聚焦方式下的三维声场能量分布
Fig. 4 3D sound field distribution of directly focusing

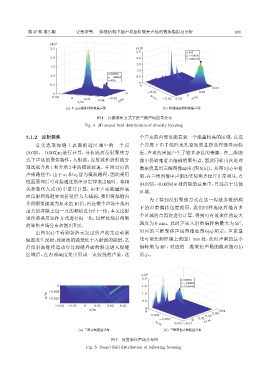
3.1.2 反射聚焦 个声束的内部也能看到一个能量较高的区域，在这

首先选取焊缝上表面附近区域中的一个点 个厚度下由于线阵元孔径较宽且距离焊缝界面较
(0.025，−0.003)m 进行计算，分析底面反射聚焦方 近，声束的周围产生了较多杂乱的旁瓣。在二维图
式下声场的聚焦特性，入射波、反射波和折射波分 像中仍较难看出准确的聚焦点，因此同样再次处理
别选取介质 1 和介质 2 中的横波波速。在图 2(b) 的 数据将其用三维图像画出(图5(b))。从图 5(b)中看
声束路径中，由于 s 1 和 s 2 皆为横波路程，因此采用 到，在三维图像中声束的实际焦点位置非常明显，点
镜面原理后可直接通过斯涅尔定律求出延时。将相
(0.0255，-0.0028)m 处的能量最集中，且远高于其他
关参数代入式 (8) 中进行计算，由于声束能量经底
区域。
面反射和焊缝界面折射后大大减弱，我们将焊缝内
为了得到反射聚焦方式在这一焊缝参数结构
介质幅值提高为原来的 10倍，再在整个声场中找出
下的声束偏转角度范围，我们同样选取焊缝内多
最大值并除上每一点的幅值进行归一化，本文反射
个区域的点再次进行计算，得到可有效聚焦的最大
聚焦都采用这种方式进行归一化，这样处理后得到
深度为 8 mm，此时声束入射的偏转角最大为 55 ，
◦
的聚焦声场分布如图5所示。
由图 5(a) 中看到各阵元发出的声波先运动到 对应的三维聚焦声场图像如图 6(a) 所示；声束最
底面发生反射，反射波的能量低于入射波的能量，之 浅可聚焦到焊缝上表面 1 mm 处，此时声束的最小
后反射波继续运动穿过焊缝界面的斜边进入焊缝 偏转角为 40 ，对应的三维聚焦声场图像如图 6(b)
◦
区域后，在内部高度集中形成一束较强的声束，这 所示。

T10 5
2.0
x: 0.02554
y: -0.00282
 1.5 z: 8.723e+04
֓⊲ 1.0
y/m ֓⊲
0.5
֓⊲ ֓⊲  ⊲ ⊲ ⊲
x/m 0 0.04
0 0.03
-0.005 0.02
-0.010 0 0.01 x/m
-0.015 -0.01
y/m
(a) ̄፥ܦڤᑟ᧚Ѭ࣋ (b) ʼ፥ᅌᓤܦڤᑟ᧚Ѭ࣋

图 5 反射聚焦声场分布图
Fig. 5 Sound field distribution of reflecting focusing