Page 90 - 201805

672 2018 年 9 月

1.2
1 引言
1.0
R
活塞式工作模式是水声领域应用最广泛的换 0.8
能器辐射类型之一，主要包括纵向换能器和厚度振 R⊳ρcS֒ X⊳ρcS 0.6
动圆片换能器等。关于活塞声源的经典研究工作比
较多，在无限大平面障板条件下，活塞声源的辐射 0.4
阻抗已经用贝塞尔函数和斯特鲁夫函数给出了解 0.2 X
析表达 [1−2] 。文献 [3] 将贝塞尔函数和斯特鲁夫函 0
0 2 4 6 8 10 12 14 16 18 20 22
数表示成高斯函数或其他简单函数的叠加，使活塞 ka
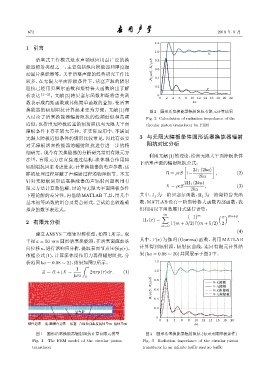
换能器的辐射阻抗计算起来更为方便。文献 [1] 深 图 2 圆形活塞换能器辐射阻抗有限元计算结果
入讨论了活塞换能器辐射阻抗的低频近似和高频 Fig. 2 Calculation of radiation impedance of the
近似，也指出无障板活塞的辐射阻抗与无限大平面 circular piston transducer by FEM
障板条件下存在较大差异。在实际应用中，不满足
无限大障板近似条件的情形比较常见，因此有必要 3 与无限大障板条件圆形活塞换能器辐射
对无障板活塞换能器的辐射阻抗进行进一步的精 阻抗对比分析
细研究。现今有关换能器的分析研究常用有限元方
利用文献[1]的理论，给出无限大平面障板条件
法 [4] ，有限元方法直接通过结构 -流体耦合作用将
下活塞声源的辐射阻抗公式：
辐射阻抗因素考虑进来，计算换能器的电声参数，这 [ ]
2J 1 (2ka)
样的处理过程屏蔽了声辐射过程的物理细节。本文 R = ρcS 1− , (2)
2ka
针对无障板圆形活塞换能器的声辐射问题利用有 2H 1 (2ka)
X = ρcS , (3)
限元方法计算数值解，讨论与无限大平面障板条件 2ka
下理论解的差异性，再借助 MATLAB工具，用几个 其中，J 1 为一阶贝塞尔函数，H 1 为一阶斯特鲁夫函
基本初等函数的组合及复合形式，尝试给出较准确 数，MATLAB没有一阶斯特鲁夫函数内部函数，我
拟合的数学表达式。 们利用以下函数展开式进行计算：
∞ m
x
∑ (−1) ( ) 2m+2
2 有限元分析 H 1 (x) = Γ(m + 3/2)Γ(m + 5/2) 2 ,
m=0
(4)
建立ANSYS 二维轴对称模型，如图 1所示。取
半径 a = 50 mm 圆形活塞换能器，在活塞面施加法 其中，Γ(x) 为伽玛 (Gamma) 函数，利用 MATLAB
向位移u，进行谐响应分析，提取表面节点压强p(r)， 计算得到辐射阻、辐射抗曲线，连同有限元计算结
依据公式 (1)，计算流体反作用力再得辐射阻抗，分 果(ka = 0.08 ∼ 20)共同展示于图3中。
析范围ka = 0.08 ∼ 21，结果如图2所示。 1.2
∫ a
1
Z = R + jX = 2πrp (r)dr. (1) 1.0
jωu 0 0.8
R⊳ρcS֒ X⊳ρcS 0.6 R-௄ᬪ౜
X-௄ᬪ౜
R-௄ᬍᬪ౜
X-௄ᬍᬪ౜
0.4

0.2
ቇඡᑿ
0
0 2 4 6 8 10 12 14 16 18 20
Ѹভ᣸ႍ ื-ڍᏹՌ᣸ႍ ำ܋ եፇ౞ᒭႀएืʹӭЋ ืʹӭЋ ka
图 1 圆形活塞换能器辐射阻抗计算有限元模型 图 3 圆形活塞换能器辐射阻抗 (有无无限障板条件)
Fig. 1 The FEM model of the circular piston Fig. 3 Radiation impedance of the circular piston
transducer transducer in an infinite baffle and no baffle