Page 91 - 201805

第 37 卷 第 5 期 莫喜平： 无障板圆形活塞换能器的辐射阻抗 673

从图 3 可以明显看出，低频 (当 ka 6 π，a 6 曲线，发现其具有以下特点：(1) 曲线存在渐近特性；

λ/2) 时，无障板的圆形活塞换能器辐射阻抗与无限 (2) 曲线具有振荡特性，且振荡幅度呈衰减规律；(3)
大障板条件下的差异较大，说明无限大障板条件的 曲线具有调频特性，且调频参数有摆动行为。
假设已经不成立了。为了进一步说明这一影响的 根据以上特点，选择处理方法和函数类型：(1)
根本原因，我们在有限元分析中提取了活塞对称轴 渐近特性：将参量减去渐近值，作为新变量参与曲线
上与活塞中心距离相等的两个点的声压幅值，其中 拟合，由图2可知，R 的渐近值R ∞ = ρcS，X 的渐近
P+为换能器前方场点的声压幅值，P−为换能器后 值 X ∞ = 0；(2) 振荡特性：用三角函数 sin x 或 cos x
方场点的声压幅值，绘制ka = 0.08 ∼ 8范围内的曲 拟合；(3) 衰减规律：用指数函数或负指数的单项式
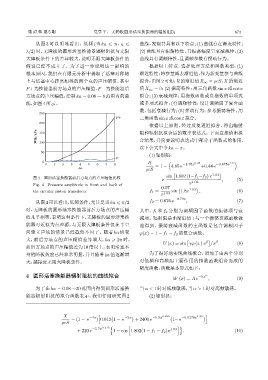
线，如图4所示。 或多项式拟合；(4) 调频特性：设计调频因子复合函
数，包括衰减行为；(5) 摆动行为：参考振荡特性，用
250
P⇁ 三角函数sin x或cos x拟合。
200
依据以上原则，经过反复逼近拟合，得出辐射
ܦԍ/kPa 150 阻和辐射抗拟合后的数学表达式。下面直接给出拟
合结果，并简要说明表达式中部分子函数式的作用，
100
以下公式中令ka = x。
50
(1)辐射阻：
P֓
0 ( )
0 1 2 3 4 5 6 7 8 R = 1 − 4.85 e −1.75x 0.25 +0.44 e −3.675x 1.6
ka ρcS
[ 1.03 ]
图 4 圆形活塞换能器前后方场点的声压幅值比较 sin 1.802 (1−f 1 −f 2 ) x (5)
× 1.03 ,
Fig. 4 Pressure amplitude in front and back of x
0.07 ( 1.03 )
the circular piston transducer f 1 = sin 1.8x , (6)
x 1.03
f 2 = 0.676 e −0.79x , (7)
从图4可以看出，低频条件，尤其是当ka 6 π/2
时，无障板的圆形活塞换能器前后方场点的声压幅 其中，f 1 和 f 2 分别为调频因子函数的振荡项与衰

值几乎相等，表明这种条件下，无障板的圆形活塞换 减项。辐射阻是由渐近值 1 与一个振荡衰减函数做
能器可近似为点声源，与无限大障板条件仅在半空 差得到，振荡衰减函数的主函数是包含调频因子
间建立声场的情景已经截然不同了。随着 ka 值变 φ(x) = 1 − f 1 − f 2 的复合函数：
大，前后方场点的声压幅值差异增大，ka > 2π 时， [ ]
β
β
U (x) = sin γφ (x ) x /x . (8)
前后方场点的声压幅值差为 10倍以上，表明活塞本
身的障板效应已经非常明显，并且随着ka值逐渐增 为了很好地实现曲线拟合，增加了由两个分别
大，越接近无限大障板条件。 对低频和高频起主要作用的指数函数组合而成的
幅度函数，函数基本形式如下：
4 圆形活塞换能器辐射阻抗的曲线拟合 −hx α
W (x) = A e , (9)
为了在 ka = 0.08 ∼20 范围内得到圆形活塞换 当α < 1时对低频敏感，当α > 1时对高频敏感。
能器辐射阻抗的拟合函数表示，我们仔细研究图 2 (2)辐射抗：

X −4x [ ( −2x ) −5.9x 0.215( −0.0278x 1.05) ]
= (1 − e ) 0.012 1 − e + 2400 e 1− e
ρcS
{ [ ]}
0.215
+ 220 e −5.7x 1 − cos 1.802(1 − f 1 − f 2 )x 1.03 . (10)