Page 92 - 201805

674 2018 年 9 月

根据辐射抗与辐射阻具有相同的周期振荡特 过一系列初等函数的复合与组合，进行曲线拟合处
性，选择相同的调频因子，其振荡衰减函数的主函数 理，最终得到一例圆形活塞换能器辐射阻抗的数学
取如下形式： 表达，通过与有限元分析结果进行比较，二者拟合度
{ [ β ] } 很好，总结全文，有以下结论：
V (x) = B e −qx τ 1− cos γφ(x )x . (11)
x β (1) 本文将有限元分析物理问题的数值解，尝
该函数有一系列 V = 0 的极小值，描述的是 试用基本数学函数进行表达，将有限元分析与数学
建模结合起来，可为结构声辐射及换能器设计建模
以 0 为 “基线” 的衰减振荡曲线。公式 (10) 中 “+”
号前面的一项主要由指数函数的组合形式构成， 提供一定的借鉴思路；
称为 “基线” 函数，将拟合曲线的基线提高，其中 (2) 本文利用初等函数的组合和复合形式将变
(1 − e −4x ) 的主要作用是对 x < 0.5 范围内进行局 化复杂的曲线用显函数形式拟合出来，得到的表
部微调。 达式虽然复杂，但每个部分函数约束曲线变化行为
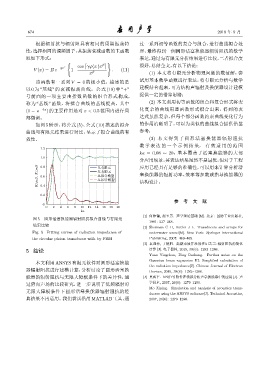
如图 5 所示，将公式 (5)、公式 (10) 描述的拟合 的作用清晰明了，可以为类似的曲线拟合提供借鉴
曲线与有限元结果进行对比，显示了拟合曲线的有 参考；
效性。 (3) 本文得到了圆形活塞换能器辐射阻抗
数 学 表 达 的 一 个 示 例 结 果， 有 效 适 用 的 范 围
1.2
ka = 0.08 ∼ 20，基本覆盖了活塞换能器的大部
1.0
分应用场景，其表达结果虽然不是最优，但对于工程
R⊳ρcS֒ X⊳ρcS 0.6 X-దᬍЋ 塞换能器的辐射功率、效率等参数或指导换能器的
应用已经具有足够的准确性，可以用来计算分析活
0.8
R-దᬍЋ
R-લՌവی
X-લՌവی
结构设计。
0.4
0.2
参 考 文 献
0
0 2 4 6 8 10 12 14 16 18 20
ka
[1] 何祚镛, 赵玉芳. 声学理论基础 [M]. 北京: 国防工业出版社,
图 5 圆形活塞换能器辐射阻抗拟合曲线与有限元
1981: 237–248.
结果比较
[2] Sherman C H, Butler J L. Transducers and arrays for
Fig. 5 Fitting curves of radiation impedance of underwater sound[M]. New York: Springer International
the circular piston transducer with by FEM Publishing, 2007: 460–465.
[3] 袁迎春, 丁德胜. 高斯束展开法的注记之三: 辐射阻抗的简化
5 结论 计算 [J]. 电子器件, 2015, 38(6): 1282–1286.
Yuan Yingchun, Ding Desheng. Further notes on the
Gaussian beam expansion III: Simplified calculation of
本文利用 ANSYS 有限元软件对圆形活塞换能
the radiation impedance[J]. Chinese Journal of Electron
器辐射阻抗进行建模计算，分析讨论了圆形活塞换 Devices, 2015, 38(6): 1282–1286.
能器的辐射阻抗与无限大障板条件下的差异性，通 [4] 莫喜平. ANSYS 软件在模拟分析声学换能器中的应用 [J]. 声
过背向声场的比较研究，进一步说明了低频辐射时 学技术, 2007, 26(6): 1279–1290.
Mo Xiping. Simulation and analysis of acoustics trans-
无限大障板条件下圆形活塞换能器辐射阻抗的经
ducers using the ANSYS software[J]. Technical Acoustics,
典结果不再适用。我们尝试借用MATLAB工具，通 2007, 26(6): 1279–1290.