Page 77 - 201806

第 37 卷 第 6 期 冯雪磊等： sinc 函数加权圆弧形恒定束宽阵列 907

其中，l 为圆弧形阵列有效部分的弧长，即l = 2α 0 r 0 。 波束宽度近似不随频率变化。
式 (11) 给出了一个估计截止频率的粗略方法，同时 进一步计算 sinc 函数加权阵列的 −6 dB 波束
式(11)提示截止频率与kl 有关。 宽度，并且分别与其他圆弧形恒定束宽阵列的波束

宽度进行对比，如图3 所示，其中黑色实线为 sinc 函
4 仿真分析
数加权阵列，黑色虚线为 Bessel 函数加权阵列，黑
为了验证本文所提出的 sinc 函数加权阵列的 色点线为 Legendre 函数加权阵列，灰色实线为余
性能，采用 Riemann 求和来近似式 (1)，分别计 弦函数加权阵列，灰色虚线为 Chebyshev 多项式加
◦
算窄覆盖和宽覆盖连续 sinc 函数加权圆弧形恒定 权阵列。图 3(a) 中的窄覆盖阵列均采用 α 0 = 15 ，
◦
束宽阵列在阵列所在平面的波束特性，如图 2 所 图 3(b) 中的宽覆盖阵列均采用 α 0 = 60 。由图 3
示。其中窄覆盖阵列对应 α 0 = 15 ，宽覆盖阵列 可见，不同阵列对应的波束宽度不同，这是由于
◦
对应 α 0 = 60 ，计算频率对应的 kl 的取值范围为 其加权函数的形状各不相同。Bessel 函数加权为
◦
10∼10000。图 2(a) 和图 2(b) 分别为窄覆盖圆弧形 f(α) = J 0 (x 0 α/α 0 )，其中 x 0 为 J 0 (x) 的最小正零
阵列和宽覆盖圆弧形阵列的三维波束图，由图 2 可 点，即 x 0 = 2.405；圆弧形 CBT 阵列采用的 Leg-
见，无论是窄覆盖阵列还是宽覆盖阵列，当 kl 大于 endre 函数加权为 f(α) = P v (cos α)，其中 P v (x) 为
某一值以后，阵列的指向性具有非常高的一致性，其 Legendre函数，且设定阶数ν 使得 α 0 为 P v (cos α)

0 -10 0
ॆʷӑSPL/dB -20 ॆʷӑSPL/dB -20
-10
-30
-30
-40
-40
-50
-60 60 90 -50 90
-60
10 1 30 10 1 30 60
10 2 0 10 2 0
-30 θ/(O) -30 θ/(O)
3
10
3
10
kl -60 kl -60
10 4 -90
10 4 -90
(a) ቌ᜸ᄦsincѦ஝ҫి᫼ѵ (b) ࠕ᜸ᄦsincѦ஝ҫి᫼ѵ
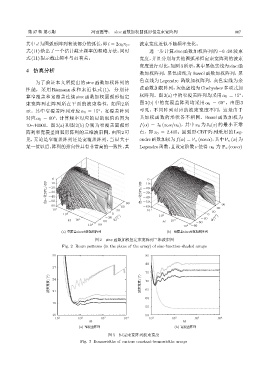
图 2 sinc 函数加权恒定束宽阵列三维波束图
Fig. 2 Beam patterns (in the plane of the array) of sinc-function-shaded arrays
30 85
80
27
75
ฉౌࠕए/(O) 24 ฉౌࠕए/(O) 70

65
21
60
18
55
15 50
10 1 10 2 10 3 10 4 10 1 10 2 10 3 10 4
kl kl
(a) ቌ᜸ᄦ᫼ѵ (b) ࠕ᜸ᄦ᫼ѵ
图 3 恒定束宽阵列波束宽度
Fig. 3 Beamwidths of various constant-beamwidthc arrays