Page 82 - 201806

912 2018 年 11 月

是不同的，而无人机声信号是平稳的，可以看作是 很多，这就意味着这种滤波方式对分布在高频部分
一种持续平稳的音素，同样可以使用 MFCC 技术 的特征并不敏感，而对于稳态强谐波分布在高频区
进行特征提取。并且针对无人机声信号与语音信 域的飞行器声信号，如果使用传统 MFCC方法进行
号的这种在平稳性方面的差异又可以对 MFCC 进 声信号的特征提取，滤波器就会像处理语音信号一
行有针对性的改进，以使其更加符合无人机声信 样进行大尺度压缩，使梅尔滤波器对分布在高频区
号频谱的分布特点。从图 4 中还可以看出，语音信 域的信号敏感度降低，从而丢失高频的稳态强谐波
号在不同时刻信号的谐波波峰对应的频率分布差 附近信号的分布特点。为了突出该类特征，使特征
距较大，在频率轴上呈现不规则的分布，而无人机 提取参数更加有效和稳定，本文针对低空飞行器声
声信号的高频段分量较多，并且无人机声信号频谱 信号的稳态强谐波特性，对梅尔滤波函数进行加权
中的谐波波峰具有明显的分布特点。这类波峰总 改进。
是在某些特定的频段附近出现，如图 4(b) 中出现在 3.2 稳态强谐波的提取与梅尔滤波器的改进

7.5 kHz∼8.5 kHz、3.5 kHz∼4.5 kHz附近，这是螺旋 声信号频谱图中的稳态强谐波携带了飞行器
桨驱动类飞行器非常重要的特点，所以应该在特征 的固有特征，比如飞行器机械结构与螺旋桨转速，能
提取过程中对无人机声信号的这种分布特点加以 否准确地定位到该类谐波所在频段是特征提取的
突出。而传统的MFCC特征提取方法使用梅尔滤波 关键。本文将多帧信号采用高阶中心滑动均值滤波
器将频率非线性地转化到梅尔域时，采用的转换函 方法进行包络提取后，对重合度高的峰值点进行提
数是固定的。从图 2 线性频率与梅尔频率转换曲线 取，定义这类峰值对应谐波为稳态强谐波。中心滑
可以看出，在高频部分，曲线的斜率相比低频部分低 动均值滤波的公式表达如下：


a+1 +i−1

 1 2 ∑ a + 1

 r(i), 1 6 i < ,

a 2

 j=1



 a+1
 i+
2
 1 ∑ a + 1 a + 1
R(i) = r(i), 6 i 6 N − , (4)
 a 2 2
 a−1

 j=i− 2


 N
 1 ∑ a + 1


 r(i), N − < i 6 N,

a 2

a+1
j=N− −i+1
2
其中，r(i)表示原始频谱序列，R(i)表示滤波后的频 根据低空飞行器结构特点，选定重复度较高的
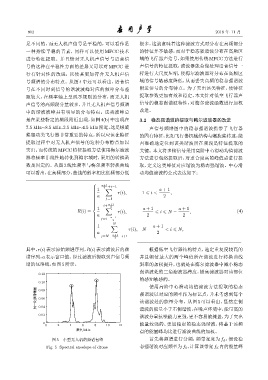
谱序列，a表示窗口值。经过滤波后提取到声信号频 并且幅值最大的两个峰值所在谐波进行转换曲线
谱的包络线，如图5所示。 斜率的加权提升，也就是在梅尔滤波器中减小稳态
强谐波处的三角滤波器跨度，提高滤波器对该部位
0.12
的感知敏感的。
0.10
使用高阶中心滑动均值滤波方法提取的稳态
ॆʷӑᮠ៨ࣨϙ 0.06 强谐波以对应的频率作为标记点，并未考虑到每个
0.08
该谐波处的能量分布。从图 5 可以看出，显然左侧
0.04
0.02 谐波的能量小于右侧谐波，在噪声环境中，能量高的
谐波分量抗噪能力更强，更不容易被掩盖，为了突出
0 能量较强的、更加稳定的稳态强谐波，将基于该频
0 2 4 6 8 10 12
ᮠဋ/kHz
点的能量峰均比进行滤波曲线的加权。
图 5 小型无人机的频谱包络 首先将频谱进行分频，频带宽度为 f d ，假设稳
Fig. 5 Spectral envelope of drone 态强谐波对应频率为 f 0 ，计算该带宽f d 内的能量峰