Page 22 - 201901

18 2019 年 1 月

其中，r 是到中心轴的距离，l 是透镜的焦距，n 0 是透 从公式 (8) 和公式 (9) 可知，密度与折射率成正
镜在中心轴的折射率。二维 Mikaelian 透镜是矩形 比，模量与折射率成反比。在本文中透镜的参数为
的，形状如图2(a)所示，其折射率可以写为 宽度d = 0.216 m，焦距为l = 0.4 m，长度为L = 4l，

n c 即透镜长度包含一个周期，如图 2(a) 所示。透镜中
n z = ( π ), (6)
cosh x 心处相对于水的折射率为 n c = 1.5，则透镜的折射
2l
其中，x为到中心轴的距离，n c 是透镜中心轴处的折 率分布n z (r)如图2(d)所示。可以看到Mikaelian透
射率，l 为透镜的焦距。 镜的折射率确实成中心轴对称分布，在中心轴处折
为了能使该透镜在水下使用，需使其与水阻抗 射率达到最大，而随着偏离中心呈反双曲余弦减小
匹配。若设水的密度为 ρ 0 、模量为 K 0 ，则其声速为 的趋势，在边缘处折射率达到 1.38 的最小值。对透
√ 镜的密度和模量进行归一化，则归一化的模量和密
c 0 = K 0 /ρ 0 ，透镜的密度记为ρ z ，模量记为K z ，则
√ 度分布如图 2(b) 和图 2(c) 所示，模量在轴心处达到
声速c z = K z /ρ z 。阻抗匹配的水下透镜的密度与
声速满足： 最小，而密度在轴心处达到最大。这与公式(8)和公
式(9)所描述的一致。
ρ z c z = ρ 0 c 0 . (7)
Mikaelian 透 镜 对 入 射 声 波 的 聚 焦 效 应 如
继而可得
图 3(a) 所示。入射声波为 160 kHz 的高斯脉冲。在
ρ 0 c 0
ρ z = = ρ 0 n z , (8) 透镜中，波束进行了两次聚焦，焦斑分别在 y = l 和
c z
2 y = 3l 处。图 3(b) 反映了在 y = l 和 y = 2l 处沿着
(ρ 0 c 0 ) K 0
K z = = . (9) 透镜宽度方向声压的幅值分布。波束在y=l 处声波
ρ z n z
1.50
y
d/⊲ m
x L/l

(a) Mikaelianᤩ᪫ᇨਓڏ 1.45
1.0
ઉ࠱ဋ

0.9 1.40
(b) ॆʷӑവ᧚Ѭ࣋
1.0

-0.1 0 0.1
0.9 x/m
(c) ॆʷӑࠛएѬ࣋ (d) ઉ࠱ဋѬ࣋

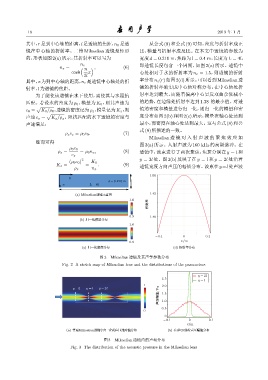
图 2 Mikaelian 透镜及其声学参数分布
Fig. 2 A sketch map of Mikaelian lens and the distributions of the parameters

y/l
y/l
2.5
y/l
y/l
1 2.0
ܦԍࣨϙ/Pa 1.5
y/ y/l y/l
1.0
0.5
0
0
-0.1 0 0.1
r/m
(a) ௿ᤰMikaelianᤩ᪫˗ॆʷӑᄊܦԍፐࠫϙѬ࣋ (b) ښl֗lܫᄊܦԍࣨϙѬ࣋

图 3 Mikaelian 透镜内的声场分布
Fig. 3 The distribution of the acoustic pressure in the Mikaelian lens