Page 24 - 201901

20 2019 年 1 月

1.5
r 2
ઉ࠱ဋ 1.2
θ  0.9

0.6
r 
0.4 0.5 0.6
r/m
(a) ऻॎMikaelianᤩ᪫ᇨਓڏ (b) ऻॎMikaelianᤩ᪫ઉ࠱ဋѬ࣋

1

0
(c) ॆʷӑവ᧚Ѭ࣋ (d) ॆʷӑࠛएѬ࣋

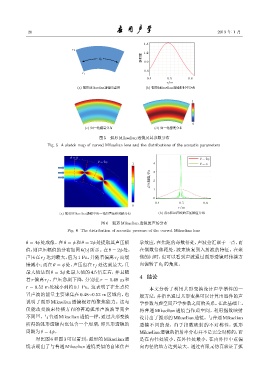
图 5 弧形 Mikaelian 透镜及其参数分布
Fig. 5 A sketch map of curved Mikaelian lens and the distributions of the acoustic parameters

图 6 弧形 Mikaelian 透镜的声场分布
Fig. 6 The distribution of acoustic pressure of the curved Mikaelian lens

θ = 4ϕ处成像。在θ = ϕ和θ = 2ϕ处提取其声压幅 学效应，在焦距的奇数倍处，声波会汇聚于一点，而
值，则声压幅值的分布如图6(b)所示。在θ = 2ϕ处， 在偶数倍焦距处，波束恢复到入射波的特征。在聚
声压在 r f 达到最大，值为 1 Pa，并随着偏离 r f 而缓 焦的同时，也可以看到声波通过弧形透镜时传播方

慢减小；而在 θ = ϕ 处，声压也在 r f 处达到最大，且 向偏转了θ 0 的角度。
最大值达到 θ = 2ϕ 处最大值的 4.5 倍左右，并且随
4 结论
着 r 偏离 r f ，声压急剧下降，分别在 r = 0.48 m 和
r = 0.52 m 处减小到约 0.1 Pa。这表明了在焦点位 本文分析了利用共形变换设计声学器件的一
置声波的能量主要聚集在 0.48∼0.52 m 区域内，也 般方法，并指出通过共形变换可以计算出器件的声
说明了弧形 Mikaelian 透镜极好的聚焦能力。这与 学参数与虚空间声学参数之间的关系。在此基础上，
仅能改变波束传播方向的普通弧形声波波导完全 将普通 Mikaelian 透镜当作虚空间，利用指数映射
不同 [9] 。与普通Mikaelian透镜一样，通过共形变换 设计出了弧形的 Mikaelian 透镜。与普通 Mikaelian
所得的弧形透镜内也包含一个周期，即共形透镜的 透镜不同的是，由于指数映射的不对称性，弧形
周期为θ = 4ϕ。 Mikaelian透镜的折射率分布并不是完全对称的，而
对比图 6 和图 3 可以看到，弧形的 Mikaelian 透 是在内径处较小，在外径处最小，在内外径中点偏
镜表现出了与普通 Mikaelian 透镜类似的自聚焦声 向内径的地方达到最大。通过有限元仿真验证了弧