Page 58 - 201901

54 2019 年 1 月

该反射器为一个放置于地面上的钝角三角形， 排列 (图 2(b))，于是在长波极限条件下可以得到该
3
空 气 的 密 度 和 模 量 分 别 为 ρ 0 = 1.21 kg/m 和 结构的等效参数：
κ 0 = 142.36 kPa。根据前文所述的变换声学方 ρ A + ρ B
ρ y = ,
′
法，可以求得其密度矩阵和模量为 2
  2ρ A ρ B
ρ x = , (7)
0.27 −1.21 0 ′
  ρ A + ρ B


ρ =  −1.21 10.89 0  , 2κ A κ B
(5) κ = .
  κ A + κ B
0 0 0.13
对于公式 (6) 中的介质而言，利用分层流体可
κ = 15.82 kPa.
以在长波极限下获得等效的各向异性密度。假设每
可见，此时密度矩阵存在非对角项，这是因为 层厚度d = 0.5 mm，则单元大小L = 1 mm。结合公
在变换声学的计算过程中，选取的是笛卡尔坐标系， 3
式(6)和公式(7)，计算可得ρ A = 21.99 kg/m ，ρ B =
该坐标系与密度矩阵的主轴方向存在一定的夹角， 0.07 kg/m 和 κ A = 2.62 MPa，κ B = 7.93 kPa。将
3
所以在矩阵中出现了非对角分量。因此，需要将密
流体 A 与流体 B 周期交错排列形成单元，并利用参
度矩阵进行旋转α = 6.42 ，从而将其中的非对角项
◦
数检索法 [25] 得到它的等效参数，以验证设计的单
消除 [9] ，得到密度矩阵的特征值：
元的有效性。检索结果如图 3 所示，图 3(a) 为厚度
 
0.13 0 0 L = 1 mm 的单元等效密度随频率变化图，其中方
 
  块和圆点标志为单元所体现出的密度，直线为器件
ρ =  0 11.03 0  ,
(6)
  设计所需的密度。可见在100 Hz∼4000 Hz范围内，
0 0 0.13
κ = 15.82 kPa. 14
12
此时，可以得到密度矩阵的主轴坐标系：将x-y
10
坐标系逆时针旋转 α = 6.42 后所得到的x -y 坐标
◦
′
′
系，如图 2(a) 所示。由求出的密度矩阵可知，在声 ࠛए/(kgSm -3 ) 8 ͌ᄾӭЋ ρ yϕ
反射器中，各个方向表现出的密度并不一样，所以 6 ͌ᄾӭЋ ρ xϕ
需要各向异性密度的流体进行实现。然而在自然 4 ٨͈ਫ਼ᭊ ρ yϕ
٨͈ਫ਼ᭊ ρ xϕ
2
界中并不存在天然各向异性的流体，因此需要引
入人工周期介质，Biot 流体理论 [6,24] 则为此提供了 0
0 1000 2000 3000 4000
可能。假设有两种不同的各向同性的流体介质 (A
ᮠဋ/Hz
和 B)，其密度和模量分别为 ρ A ，ρ B 和 κ A ，κ B 。在 (a) ӭЋࠛएᬤᮠဋԫӑ
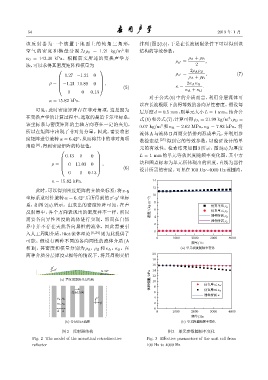
两种介质分层厚度 d 相等的情况下，将其周期交错 20
18
16
yϕ
xϕ 14
⊲O
ʹሥവ᧚/kPa 10 ͌ᄾӭЋ κ xϕ
(a) ܦԦ࠱٨ᄊѬࡏፇ౞ 12
ѬࡏவՔ 8 6 ͌ᄾӭЋ κ yϕ
٨͈ਫ਼ᭊ κ
xϕ 4
ρ A ρ B
yϕ 2
κ A κ B
0
d d 0 1000 2000 3000 4000
ᮠဋ/Hz
(b) ѬࡏBiotืʹ (b) ӭЋവ᧚ᬤᮠဋԫӑ
图 2 反射器结构 图 3 单元参数随频率变化
Fig. 2 The model of the acoustical retrodirective Fig. 3 Effective parameters of the unit cell from
reflector 100 Hz to 4000 Hz