Page 54 - 201901

50 2019 年 1 月

25 25
FDFxLMS 20 FDFxLMS
20 Leaky Leaky
cFDFxLMS 15 cFDFxLMS
15
10
ᬌ٪᧚/dB 5 ᬌ٪᧚/dB 5 0
10

-5
0
-10
-5
-15
-10 -20
0 1 2 3 4 5 6 7 8 0 1 2 3 4 5 6 7 8
ᮠဋ/kHz ᮠဋ/kHz
(a) Яവی଍҄Ԧᯠጇፒ (b) እӑԦᯠጇፒ

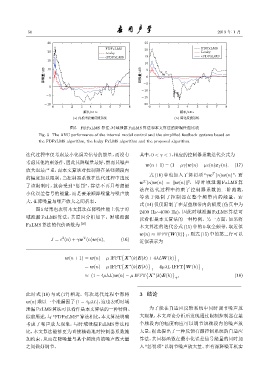
图 5 FDFxLMS 算法、时域泄露 FxLMS 算法和本文算法的降噪性能比较
Fig. 5 The ANC performance of the internal model control and the simplified feedback systems based on
the FDFxLMS algorithm, the leaky FxLMS algorithm and the proposed algorithm.

迭代过程中仅考虑最小化误差信号的能量，而没有 其中，0 < γ < 1，相应的控制器系数迭代公式为
考虑其他约束条件，因此其降噪量最好，然而其噪声
w(n + 1) = (1 − µγ)w(n) − µe(n)x f (n). (17)
放大也最严重，而本文算法对控制器在某些频段内
T
式 (16) 中也加入了惩罚项 “γw (n)w(n)”，而
的幅度加以限制，当控制器系数在迭代过程中违反
w (n)w(n) = ∥w(n)∥ ，即时域泄漏 FxLMS 算
2
T
了该限制时，就会受到 “惩罚”，算法不再只考虑最
法在迭代过程中约束了控制器系数的二阶范数，
小化误差信号的能量，而是要兼顾降噪量与噪声放
等效于限制了控制器在整个频带内的能量，而
大，在降噪量与噪声放大之间折衷。
式 (14) 仅仅限制了在某些频带内的幅度 (仿真中为
图5 结果也表明本文算法在降噪性能上优于时
2400 Hz∼4000 Hz)，因此时域泄漏 FxLMS 算法可
域泄漏 FxLMS 算法，其原因分析如下。时域泄漏
以看作是本文算法的一种特例。另一方面，如果将
FxLMS算法的代价函数为 [16] 本文算法的迭代公式 (15) 中的 k 取全频带，取近似
w(n) ≈ IFFT{W (k)} + ，则式 (15) 中的第二行可以
T
2
J = e (n) + γw (n)w(n), (16)
近似表示为
{ }
∗
w(n + 1) = w(n) − µ IFFT X (k)E(k) + 4λLW (k)
+
{ } { }
∗
= w(n) − µ IFFT X (k)E(k) − 4µλL IFFT W (k)
+ +
{ }
∗
≈ (1 − 4µλL)w(n) − µ IFFT X (k)E(k) , (18)
+
此时式 (18) 与式 (17) 相近，每次迭代过程中都将 3 结论
w(n)乘以一个泄漏因子(1 − 4µλL)，这也表明时域
泄漏FxLMS算法可以看作是本文算法的一种特例。 为了能在自适应反馈系统中同时调节噪声放
综前所述，与“FDFxLMS”算法相比，本文算法明确 大现象，本文理论分析后发现通过限制控制器在某
考虑了噪声放大现象，与时域泄漏 FxLMS 算法相 个频段内的幅度响应可以调节该频段内的噪声放
比，本文算法能够更为直接精确地对控制器系数施 大量，据此提出了一种反馈有源控制系统的自适应
加约束，从而在降噪量与某个频段内的噪声放大量 算法，其目标函数在最小化误差信号能量的同时加
之间做好调节。 入“惩罚项”以调节噪声放大量。在有源降噪耳机实