Page 36 - 应用声学2019年第4期

496 2019 年 7 月

-50 -50
850 850
-55 -55
800 800
-60 -60
750 750
ᮠဋ/Hz 700 -65 ฉ஝៨/dB ᮠဋ/Hz 700 -65 ฉ஝៨/dB
650
-70 650 -70
600 600
-75 -75
550 550
500 -80 500 -80
0.5 1.0 1.5 2.0 0.5 1.0 1.5 2.0
ฉ஝ ฉ஝
(a) ܦູງए7 m (b) ܦູງए50 m

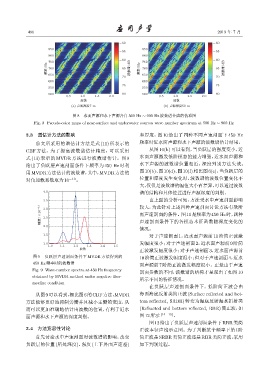
图 8 水面声源和水下声源各自 500 Hz ∼ 900 Hz 波数谱合成的伪彩图
Fig. 8 Pseudo-color maps of near-surface and underwater sources wave number spectrum at 500 Hz ∼ 900 Hz

3.3 谱估计方法的影响 和厚度，图 10 给出了四种不同声速剖面下 450 Hz
前文所采用的谱估计方法是式 (11) 所表示的 频率时近水面声源和水下声源的波数谱估计结果。
CBF 方法，为了提高波数谱估计精度，可以采用 从图 10(h) 可以看到，当负跃层的强度变小，近
式 (13) 表示的 MVDR 方法进行波数谱估计。图 9 水面声源激发低阶模态的能力增强，近水面声源和
给出了负跃层声速剖面条件下频率为 450 Hz 时利 水下声源的波数谱位置相近，深度判别方法失效。
用MVDR方法估计的波数谱，其中，MVDR 方法的 图10(b)、图10(d)、图10(f) 相比图 6(c)，当负跃层的
对角加载系数取为10 −10 。 位置和厚度发生变化时，波数谱的波数位置变化不
大，仅仅是波数谱的幅值大小有差异，可以通过波数
4.0 谱的结构和具体位置进行声源深度的判别。
由上面的分析可知，方法受水中声速剖面影响
3.5 较大，为此针对上述四种声速剖面讨论方法有效所
ࣨए/T10 -11 3.0 需声速剖面的条件。图11是频率为450 Hz时，四种

2.5
2.0 声速剖面条件下的各模态本征函数随深度变化的
情况。
1.5 对于声速剖面 1，近水面声源前 11 阶简正波激
1.0 发幅度很小；对于声速剖面 2，近水面声源前 9 阶简
1.0 1.1 1.2 1.3 1.4 1.5
⌒ᮠ 正波激发幅度很小；对于声速剖面3，近水面声源前
图 9 负跃层声速剖面条件下 MVDR 方法得到的 10阶简正波激发幅度很小；但对于声速剖面 4，近水
450 Hz 频率时的波数谱 面声源前 7 阶简正波激发幅度很小。正是由于声速
Fig. 9 Wave-number spectra at 450 Hz frequency
剖面参数的不同，波数谱的结构才呈现出了如图 10
obtained by MVDR method under negative ther-
所示不同的特征情况。
mocline condition
在负跃层声速剖面条件下，低阶简正波会由
从图9可以看到，相比图6的CBF方法，MVDR 海面海底反射类简正波 (Surface reflected and bot-
方法能够更好地抑制旁瓣并且减小主瓣的宽度，从 tom reflected, SRBR) 转变为海底反射海水折射类
而可以更加准确地估计出波数的位置，有利于近水 (Refracted and bottom reflected, RBR)简正波，如
面声源和水下声源的深度判别。 图12所示 [14−15] 。
图12给出了负跃层声速剖面条件下RBR 类简
3.4 方法宽容性讨论 正波本征声线示意图。为了判断某个频率下第 l 阶

首先讨论水中声速剖面对波数谱的影响，改变 简正波是SRBR类简正波还是RBR类简正波，采用
负跃层的位置 (所处深度)、强度 (上下界面声速差) 如下判别过程。