Page 32 - 应用声学2019年第4期

492 2019 年 7 月

里叶变换，得到每个频率具有 L 次快拍的频域数据 0
模型。在已知到达角θ 时，对波数k 进行搜索。
20
H
B sum (f, k) = ω (k)R Y (f)ω(k). (11)
40
ງए/m
当k = k rm 时，各个阵元的第 m阶简正波同相相加，
而其他阶简正波由于非完全同相而被不同程度地 60
80
抑制。这样就可以得到该频率下的波数谱，在 k rm
处的谱峰的幅度就是第m阶简正波的幅度。
100
式 (11) 属 于 常 规 波 束 形 成 (Conventional 1460 1470 1480 1490 1500 1510 1520 1530 1540
ܦᤴ/(m⋅s -1 )
beamforming, CBF) 方法。为了提高谱估计的分
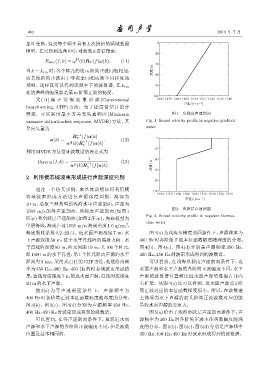
辨率，可以采用最小方差无失真响应 (Minimum 图 1 负梯度声速剖面
variance distortionless response, MVDR) 方法，其 Fig. 1 Sound velocity profile in negative gradient
导向矢量为 water
R −1 (f)a(k) 0
ω(k) = Y −1 . (12)
H
a (k)R (f)a(k)
Y
20
利用MVDR方法估计波数谱的表达式为
1
B MVDR (f, k) = −1 . (13)
H
a (k)R (f)a(k) ງए/m 40
Y 60
2 利用模态域波束形成进行声源深度判别
80
通过一个仿真示例，来具体说明如何利用模 100
1460 1470 1480 1490 1500 1510 1520 1530 1540
态域波束形成方法进行声源深度判别。海深为
ܦᤴ/(m⋅s -1 )
10 m，选取三种典型的浅海水中声速剖面：声速为
图 2 负跃层声速剖面
1500 m/s 的等声速剖面、负梯度声速剖面 (如图 1
Fig. 2 Sound velocity profile in negative thermo-
所示)和负跃层声速剖面(如图2所示)。海底模型为
cline water
3
单层海底，海底声速1650 m/s，海底密度1.6 g/cm ，
海底吸收系数 0.2 dB/λ。近水面声源深度 7 m，水 图 4(a) 为浅海负梯度剖面条件下，声源频率为
下声源深度 50 m，位于水平直线阵的端射方向。水 400 Hz 时各阶简正波本征函数幅度随深度的分布。
平直线阵深度 80 m，阵元间距10 m，共100 个阵元， 图 4(b)、图 4(c)、图 4(d) 分别是声源频率 350 Hz、
即1000 m 的水平孔径，第1 个阵元距离声源的水平 400 Hz、450 Hz时波束形成得到的波数谱。
距离为3 km。采用式(11)的CBF方法，处理给出频 可以看到，在浅海负梯度声速剖面条件下，近
率为 350 Hz、400 Hz、450 Hz 的模态域波束形成结 水面声源和水下声源的各阶简正波幅度不同，水下
果，蓝线对应深度7 m的近水面声源，红线对应深度 声源的波数谱位置相比近水面声源明显偏右并向
50 m的水下声源。 右扩展。从图 4(a) 还可以看到，近水面声源前 5 阶
图 3(a) 为等声速剖面条件下， 声源频率为 简正波对应的本征函数幅度很小。所以，在波数谱
400 Hz 时各阶简正波本征函数幅度随深度的分布。 上体现为水下声源的前几阶简正波波数对应的能
图 3(b)、图 3(c)、图 3(d) 分别为声源频率 350 Hz、 量较水面声源的要更大。
400 Hz、450 Hz时波束形成得到的波数谱。 图 5(a) 给出了浅海负跃层声速剖面条件下，声
可以看到，在等声速剖面条件下，虽然近水面 源频率为 400 Hz 时各阶简正波本征函数幅度随深
声源和水下声源的各阶简正波幅度不同，但是波数 度的分布。图5(b)、图5(c)、图5(d)分别是声源频率
位置是基本相同的。 350 Hz、400 Hz、450 Hz时波束形成得到的波数谱。