Page 81 - 应用声学2019年第5期

第 38 卷 第 5 期 孟庆波等： 深度约束下的声速估算 833

4 初始计算时声速为表层声速 1538.903 m/s，ε
2 ඵʾऄን٨ 1
3 ๒᭧๏ಖ 值的设定为0.001，即计算的深度与实际深度约束给
2
出的差值在 ±1 mm 范围内时的声速为最终估计声
1 速。选取浮标1 和水下目标 A 进行估算，表 1 和图 6
y/km 0 表示了每次迭代中的声速改正值及声速的变化曲

-1
线。从表 1 可以得出，经过10次迭代声速趋于稳定，
-2
前四次迭代中，声速的改正数比较大，说明此时与实
-3
3 4 际有效声速相差比较大，随着迭代次数的增加，声速
-4
-5 -4 -3 -2 -1 0 1 2 3 4 5 越来越接近实际有效声速，改正数值逐渐减少，最
x/km
终迭代终止声速为 1493.534 m/s，在图 6 中也可以
图 4 浮标及水下目标模拟位置示意图
看出，当迭代次数到达5 次以后时，声速曲线波动较
Fig. 4 Buoy and underwater target simulation position
小，近乎平直，改正值在0.1 m/s内。
表2记录的是每次迭代次数中水下应答器坐标
2004
ԍҧ͜ਖ٨ງए 与其真值的差值，可以看出随着迭代次数的增加，计
2003
໚ฉՑງए
2002 算的深度与实际深度平面之间的差值越来越小，逐
步收敛满足限差要求。结合表 1 可以看出，在每次
2001
ງए/m 2000 的迭代计算中若计算的深度值大于实际深度值时，

1999 声速的改正为负数；若计算深度值小于实际的深度
1998 值时，改正为正数，验证了本文方法思路是正确有
1997 效的。
1996 为了验证最终估计声速是否满足定位需求，将
10 20 30 40 50 60 70 80 90 100
ԋЋ˔஝/˔ 本文方法所得声速与加权平均声速法、泰勒级数
图 5 压力传感器深度及滤波后深度 展开法、等效声速法对四个水下应答器的定位结果
Fig. 5 Pressure sensor depth and post-filter depth 进行了比较，分别统计每个浮标 X、Y 、Z 方向上

相对于坐标真值的差异 ∆X、∆Y 、∆Z，结果如图 7
1540 所示。同时计算了四种方法的定位均方根 (Root

1530 mean square，RMS)值。本文方法定位结果的 RMS
为0.671 m，加权平均声速法、泰勒级数展开法、等效
ܦᤴ/(mSs -1 ) 1520 声速法三种方法的 RMS 分别为 1.523 m、0.723 m、
1510
0.885 m。从均方根大小以及图7可以得出本文提出
1500
的方法所估计的声速满足定位需求，定位结果优于
1490 其他三种方法。其中水平 XY 方向的定位精度与泰
勒级数展开方法、等效声速法接近，远高于加权平
1480
1 2 3 4 5 6 7 8 9 10
ᤖ̽൓஝ 均声速法的定位结果，在垂直 Z 方向上，由于本文
方法使用了深度约束，垂直方向定位精度远高于其
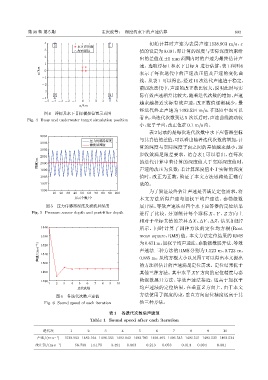
图 6 各迭代次数声速值
Fig. 6 Sound speed of each iteration 他三种方法。

表 1 各迭代次数后声速值
Table 1 Sound speed after each iteration

䘝ԓ⅑ 1 2 3 4 5 6 7 8 9 10
༠䙏/(mSs -1 ) 1538.903 1482.164 1496.333 1492.842 1493.705 1493.492 1493.545 1493.531 1493.535 1493.534
᭩↓٬/(mSs -1 ) -56.738 14.170 -3.491 0.863 -0.213 0.053 -0.014 0.004 -0.001