Page 83 - 应用声学2019年第5期

第 38 卷 第 5 期 孟庆波等： 深度约束下的声速估算 835

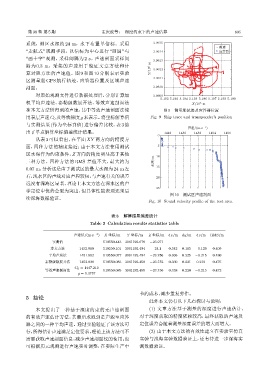
系统，测区水深约 24 m，水下布置单信标。采用 3.9615
ᓕᤜ
“走航式” 观测手段，以信标为中心进行 “画圆” 与 3.9614 ऄን٨

“画十字” 观测，采样间隔为 2 s。声速剖面采样间
3.9613
隔为 0.3 m，采集的声速用于验证文章方法和计 Y/10 6 m 3.9612
算对照方法的声速值。图 9 和图 10 分别表示实验
3.9611
区测量船 GPS 航行轨迹、应答器位置及区域声速
剖面。 3.9610
对原始观测文件进行数据处理后，分别计算加 3.9609
5.192 5.193 5.194 5.195 5.196 5.197 5.198 5.199
权平均声速法、泰勒级数展开法、等效声速剖面法 X/10 m
5
和本文方法所得到的声速，其中等效声速剖面法使 图 9 测量船轨迹及应答器位置
用表层声速C 0 及等效梯度g 来表示。将坐标解算值 Fig. 9 Ship trace and transponder’s position
与实测结果 (作为坐标真值) 进行偏差比较，表 3 给
ܦᤴ/(mSs -1 )
出了单点解算坐标偏差统计结果。 1448 1450 1452 1454 1456
0
从表 3 可以看出，在平面 XY 两方向的精度方
面，四种方法的精度接近；由于本文方法使用测试 5
区水深作为约束条件，Z 方向的精度明显高于其他 10
ඵງ/m
三种方法。四种方法的 RMS 差值不大，最大约为
0.07 m，分析这是由于测试区的最大水深为24 m左 15
右，浅水区的声线对应声程较短，与声速有关的误差 20
远没有深海区显著，理论上本文方法在深水区的声
25
学定位中优势会更为突出，但具体性能表现还须后
图 10 测试区声速剖面
续深海数据验证。
Fig. 10 Sound velocity profile of the test area

表 3 解算结果偏差统计
Table 3 Calculation results statistics table

声速值/(m·s −1 ) X 坐标/m Y 坐标/m Z 坐标/m dx/m dy/m dz/m RMS/m
实测值 519550.443 3961192.679 −23.971
本文方法 1452.989 519550.101 3961192.494 −24.1 0.342 0.185 −0.129 0.409
平均声速法 1451.882 519550.077 3961192.454 −23.756 0.366 0.225 −0.215 0.480
泰勒级数展开法 1452.838 519550.083 3961192.458 −23.752 0.360 0.221 0.219 0.475
C 0 = 1447.210
等效声速剖面法 519550.085 3961192.459 −23.756 0.358 0.220 −0.215 0.472
g = 0.4757

节约成本，减少重复劳作。
5 结论
此外本文仍有以下几点探讨与说明：
本文提出了一种基于深度约束的无声速剖面 (1) 文章方法基于测量的深度进行声速估计，
的有效声速估计方法，其最后求取到是声源至应答 对于深度获取的精度依赖较高，最终获取的声速及
器之间的一种平均声速。通过实验验证了该方法可 定位误差会随着测量深度误差的增大而增大。
行，所得估计声速满足定位要求，理论上该方法可不 (2) 由于本文方法的有效性建立在实验室仿真
需要获取声速剖面信息，减少声速剖面仪的使用；也 实验与浅海实验数据验证上，还有待进一步深海实
可根据历元观测进行声速实时调整，在实际生产中 测数据验证。